Double reed acoustics: oboe, bassoon and others

Overview

The reed controls the air flow

Let's imagine steady flow with no vibration and no resonator, and graph how air flow through the reed depends on the difference in pressure between the player's mouth and the volume inside the reed. If you increase this pressure difference, more air should flow through the narrow aperture between the reed blades. So a graph of flow vs pressure difference rises quickly: it has positive slope, as sketched below on the left of the graph.

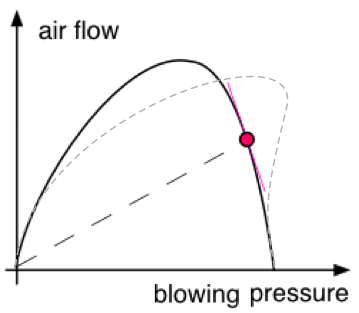
However, as the mouth pressure gets large, it starts to flatten the reed blades and so tends to close the aperture through which the air is entering. Indeed, if you blow hard enough, it closes completely, and the flow goes to zero. So the flow-pressure diagram looks like that in the (highly simplified) diagram. Different curves are possible, depending on the stiffness and shape of the blades, and on the embouchure forces: vertical lip forces tend to close the aperture and lower the curve overall; 'pushing in' with horizontal forces tends to open it. Adjustment with the reed knife changes the reed mechanics and so also changes this curve in important ways. The curve is complicated by other effects. The air travels rapidly through the reed, which produces a suction that helps to close the blades. Further, as the blades close, their curvature is reduced, which reduces their effective stiffness. So the reed tends to close easily and abruptly at the right hand side of the curve, which has important consequences. The solid curve sketched above neglects air resistance in the channel, which can bend the peak of the curve to the right (dashed curve), and reduce the negative resistance region, but allow the reed to oscillate between a closed and open state when matched to a suitable bore. This 'beating reed' (closing completely for a short section of the cycle) is common in normal double reed performance; it contributes high harmonics and thus the bright timbre of double reed instruments.

The player provides power via a flow of air at pressure above atmospheric: this is the source of energy, but it is (more or less) steady. What converts steady power (DC) into acoustic power (AC) is the reed. The left side of the graph is something like a resistance: flow increases with increasing pressure difference (DC electrical current increases with increasing DC voltage). Just like an electrical resistance, an acoustic resistor loses power. So in this regime, the instrument will not play, though there is some breathy noise as air flows turbulently through the reed aperture. The operating regime is the downward sloping part of the right hand side of the curve in the sketch above. This is related to why there is both a minimum and maximum pressure (for any given reed) that will play a note. Blow too softly and you get air noise (left side of the graph), blow very hard and it closes up (where the graph meets the axis on the right).

Consider the red dot as an operating point. Readers with a background in electricity, seeing this region of the curve in which flow decreases with increasing pressure, will recognise this as a negative AC resistance—the inverse slope of the red line. Whereas a positive resistance takes energy out of a circuit, a negative resistance puts energy into the circuit (as happens in e.g. a tunnel diode oscillator). Note that the DC resistance (inverse slope of the dashed straight line) is positive. In the instrument, the positive DC resistance takes energy out of the DC air flow and it is indeed this negative AC resistance that provides the AC energy lost in the rest of the instrument. Most of the energy is lost inside the bore, in viscous and thermal losses to the walls, and a relatively small fraction is emitted as radiated sound.

Another way of understanding the active role of the reed is to consider a small wave of excess pressure arriving from the bore into the reed. This opens the reed aperture a little, letting in more high-presssure air from the player's mouth. That extra air raises the pressure in the reed still further, so a larger pressure wave is reflected back down the bore. Conversely, a negative pressure wave arriving in the reed closes the aperture a little, reducing the flow and futher reducing the pressure. So, with appropriate blowing pressure, embouchure forces and reed properties, the reed provides positive gain: it tends to amplify sound vibrations in the bore. The stroboscopic video below was made by scientist and oboist Leonardo Fuks. (The upper joint of the oboe, finger holes closed, was connected at the joint end to a volume of air at less than atmospheric pressure. The reed (and camera) were in the air of the laboratory. This set-up played a note near G4.)

Articulation

Playing softly and loudly

Control parameters for playing

For any given fingering, reed and mouthpiece set-up, the player can make a range of sounds, varying the pitch, loudness and spectrum. Various control parameters are available to the player: pressure in the mouth can be varied, so can the lip forces in the vertical and horizontal directions, the position at which the lip presses on the reed, and sometimes the configuration of the vocal tract. We have investigated these parameters mainly on the clarinet. One reason is that we understand the (simpler) clarinet reed better than the double reed. Another is that we have a robot clarinet player in which we can vary all these parameters in a controlled way. We report these results in more detail on the clarinet robot site, along with links to scientific reports on that project. A big difference, however, is the application of horizontal lip forces on the double reed; these allow the player to vary the effective stiffness of the reed.

Pressure, air flow and speed. It's worth mentioning that, among woodwind instruments, the blowing pressure for oboes is sometimes very high (possibly above 10 kPa for a loud high note). Nevertheless, the rate of flow into the instrument is relatively low, because the gap between the blades of the reed is small. So an oboist can sustain a note for a long time. The low register of the bassoon, in contrast, can accept relatively high rates of flow, especially when playing loudly. We have a separate page on air speed, air flow, pressure and power in woodwind and brass instruments.

A warning for oboists: sustained very high pressures are reported to affect circulation in the head and neck, with reports of possible consequences including stroke and eye damage. Be careful, and avoid very hard reeds. Also, the fact that you can play very long soft passages without breathing doesn't mean that you should: if the conductor goes blurry, you are about to faint.

Oboes and bassoons as 'closed' pipes

For the purposes of this simple introduction to double reed acoustics, we shall now make some strong approximations. First, we shall pretend that it is a simple conical pipe – in other words we shall assume that all holes are closed (down to a certain point, at least), that the bore is conical, and that the mouthpiece end is completely closed. This is a crude approximation, but it preserves much of the essential physics, and it is easier to discuss.

The natural vibrations of the air in the instrument, the ones that cause it to play notes, are due to standing waves. (If you'd like an introduction to this important concept, see standing waves.) What are the standing waves that are possible in such a tube?

To answer the question, we must take into account the fact that the instrument is approximately conical. This means that sound waves 'spread out' as they travel down the bell. This means that the amplitude of travelling waves gets smaller as we go from mouthpiece to bell. The fact that the instrument is open to the air at the far end means that the total pressure at that end of the pipe must be approximately atmospheric pressure. In other words, the acoustic pressure (the variation in pressure due to sound waves) is approximately zero (called a pressure node). The mouthpiece end, on the other hand, can have a maximum variation in pressure: it is an antinode in pressure. If we were dealing with a cylindrical pipe (such as a flute or clarinet), where the standing waves are sinusoidal, we would expect the maximum and the zero of a wave to be one quarter wavelength apart. But the variation in the amplitude of the wave due to the variation in cross sectional area complicates the story.

So we have devoted a whole page to comparing cylindrical and conical pipes and, if you want the details, you should read that page now. However, the result is this: the standing waves in a cone of length L have wavelengths of 2L, L, 2L/3, L/2, 2L/5... in other words 2L/n, where n is a whole number. The wave with wavelength 2L is called the fundamental, that with 2L/2 is called the second harmonic, and that with 2L/n the nth harmonic. The frequency equals the wave speed divided by the wavelength, so this longest wave corresponds to the lowest note on the instrument: Bb1 on a bassoon, E3 on a cor anglais and Bb3 on an oboe. (You can check the frequencies of notes on the note table.) You might want to measure the length of your instrument, take v = 345 m/s for sound in warm, moist air, and calculate the expected frequency. The calculation setting L = v/2f doesn't give you the real length of the instrument. Rather it gives the length of the cone made by removing the reed and extrapolating the taper of the bore back to a point, which is considerably longer than the geometrical length. An important point about the bassoon is that its bore can be modified by the user to a substantial extent by replacing the crook (bocal), which is a non-negligible fraction of the effective length, particularly for high notes, and whose diameter significantly affects performance. Professionals often have several crooks and change among them, sometimes in the same piece: one may play more safely in the high passages while another sounds better or is easier to play in tune. Harmonics So, with all of the tone holes closed, an oboe or bassoon can play the lowest note (Bb3 or Bb1) with a wavelength somewhat more than twice the length of the instrument. With this fingering, however, it can also play other notes by overblowing – by changing your embouchure and blowing pressure and selecting a different resonance. The harmonic series on Bb3 is shown below. For the bassoon, transpose this down two octaves. (Note that the 7f doesn't fit into the usual scale; G half-sharp is a reasonable approximation.)

How the reed and bore work together

When the instrument is playing, the reed is vibrating at one particular frequency. But, especially if the vibration is large, as it is when playing even a little loudly, it generates harmonics (see What is a sound spectrum?). These set up, and are in turn reinforced by, standing waves. Consequently, the sound spectrum has strong components at harmonics of the fundamental being played. For notes in the low range of the instrument, there are usually resonances at the frequencies of some of the harmonics. These result in greater radiation of the sound at those frequencies. In the high range of the instrument, the higher resonances do not systematically fall near harmonics of the note being played.

Sound spectra

In the section on standing waves, each wave is considered as a pure sine wave. The sound of a wind instrument can bea little like a sine wave when played very softly, but successively less like it as it is played louder. To make a repeated or periodic wave that is not a simple sine wave, one can add sine waves from the harmonic series. So the played note C4 contains some vibration at C4 (f_o), some at C5 (2f_o), some at G5 (3f_o) etc. The 'recipe' of the sound in terms of its component frequencies is called its sound spectrum.

For double reeds, the low harmonics are all strong, and some may be stronger than the fundamental. Above the cutoff frequency, the amplitude of the harmonics decreases with increasing frequency. (The researcher Lehman has identified two formants in the bassoon spectrum, at frequencies of 440-500 Hz and 1220-1280 Hz, which is a point near the middle of the (human) vowel plane.)

Opening tone holes

For the moment, we can say the an open tone hole is almost like a 'short circuit' to the outside air, so the first open tone hole acts approximately as though the instrument were 'sawn off' near the location of the tone hole. This approximation is crude, and in practice the wave extends somewhat beyond the first open tone hole: an end effect. (More about this below.)

(For the technically minded, we could continue the electrical analogy by saying that the air in the open tone hole has inertia and is therefore actually more like a low value inductance. The impedance of an inductor in electricity, or an inertance in acoustics, is proportional to frequency. So the tone hole behaves more like a short circuit at low frequencies than at high. This leads to the possibility of cross fingering, which we have studied in more detail by comparing modern, classical and baroque flutes.)

The frequency dependence of this end effect means that the higher note played with a particular fingering has a larger end effect than does the corresponding note in the lower register. If the instrument really were a perfect cone with tone holes, then the registers would be out of tune: the intervals would be too narrow. This effect is removed primarily by subtle variations in the shape of the bore, the volume of air in the reed and the flexibility of the reed blades.

The bassoon's tone holes are unusual in that, over most of the range, they are long. This photo of the tenor joint shows the 'wing': a thickening in the tube wall. I have inserted straws in the three left hand fingerholes to show the angle at which they are drilled (dashed lines superposed). The length and these angles allow holes that are widely separated in the bore to be brought within reach of the fingers. Their extreme length lowers the cut-off frequency and allows cross fingering in the first register (e.g. LH XOX for Eb3) —which is not possible on other modern woodwinds but normal in baroque instruments. This photo also shows that the cone angle is small and that an extrapolation of the cone to a point would go well past the reed.

The very long chimneys on the wing joint of the bassoon (figure above) have another effect when they are closed. Consider the frequency for which the length of the closed chimney is one quarter of a wavelength. Where it meets the bore, this 'quarter wave stub' (as an engineer would say) has a minimum in acoustic impedance and so short circuits the bore. This frequency is much higher than any fundamental on the bassoon, but it should act as a filter on a harmonic of some notes.

Register holes

A small hole can serve as a register hole. For instance, if you play E4 on an oboe (call this frequency f_o) and then push the first octave key, you are opening a hole part way down the (closed part of the) instrument. This hole disturbs the resonance that supports the fundamental of E4, but has little effect on the higher harmonics, so the instrument 'jumps up' to E5 (2f_o). The oboe has a further one or two register keys, and the option of part opening the LH index finger as a further register hole. The bassoon also has three register keys for the left thumb, and also uses part uncovering ('half-holing') of a tone hole by the LH index finger and the whisper key.

The first mode of vibration is used for the range Bb3 to C5 on oboe and Bb1 to F3 on bassoon. The second mode is used for C#5 to C6 and F#3 to D4 on those instruments. As register keys, the first few notes use the LH index (which is conveniently near the effective half-way position and so works well, especially if the finger can vary the opening size) then the octave key(s) (oboe) and whisper key (bassoon) (which work as compromises over a larger range of pitch). For the third and higher modes, it becomes complicated: tone holes contribute as register holes (e.g. LH1 for C#6 on oboe and D#4 for bassoon), along with dedicated register keys.

Where to put a register key? The acoustically obvious place to put a register hole is at a pressure node of the upper note which is also a region of large pressure variation for the lower note. Opening the bore to atmospheric pressure at a pressure node makes no difference to that note. One problem is that each note in the upper register has its pressure node at a different position. One can imagine an instrument that had a separate register hole for each note, but that would be a lot of keys. Counting the half-holing of the LH index finger, the oboe has three or four register holes, and the bassoon five, while tone holes also serve in this role. (Arlen Fast is working with the Fox company to add more to the contrabassoon, and spent time in our lab on this project.) Using one register hole for several notes is a compromise: it is not quite at the pressure node of the standing wave of the required upper note. This is not a big problem in practice. The register hole is small, so it is not really a 'short circuit', except at low frequencies. So it does not too much affect the higher frequency standing waves. (We explain how the mass of the air seals the hole at high frequencies below.) It does however disrupt the fundamental (or other low mode), and that is its purpose: to stop the instrument dropping down to its bottom register.

Ideally, there is one obvious place to put a register hole for the second mode: halfway along the effective acoustic length. For the third mode, one third and also two thirds of the way are possible. The latter solution is less attractive, however, in that it will work for a smaller range of notes than will a hole at one third of the way along.

The bassoon regularly uses a technique called flicking, which is rarely used on other winds. For notes in the third octave and higher, a register key that would perturb the intonation or timbre of a sustained note is flicked open briefly as the note is started to avoid having the note 'drop' to a lower resonance.

(The operation of two of the octave octave keys is partially automated on some oboes (and fully automated on the saxophone and the Fast system contrabassoon): one key opens one or other of two register holes, according to whether or not the third finger of the left hand is depressed. This is an example of a mechanical logic gate. Register holes are discussed in more detail on the page about clarinet acoustics. See more about register holes on the clarinet page.)

Cross fingering

On the oboe, successive semitones are usually played by opening a tone hole dedicated to that purpose. Being a closed, conical pipe, the oboe and bassoon overblow an octave, and so one would need twelve tone holes to cover the keys in one octave before repeating fingerings using the octave key for the register holes. Because players don't have this many fingers, the keys and clutch mechanisms are supplied, so that one finger can close or open two or more holes. The oboe fingering system is somewhat similar to that developed by Theobald Boehm for the flute (and largely followed on the clarinet and saxophone). Where cross fingering is used on the oboe, it is usually used to control other keys. For instance, one of the fingerings for the note F4 or F5 is the same as that for E4 or E5 plus one other opened tone hole. Another fingering 'feels like' a cross fingering (XXX|XOX). However, in that fingering the RH ring finger key has a link that closes another key above the open middle-finger hole. (The Viennese oboe uses cross fingering a little more than the standard oboe, beginning at Bb5 rather than C#6. Bassoon cross fingerings also commence near the top of the second register, at Eb4.)

The bassoon is more complicated and doesn't follow the Boehm system. First, the tone holes are often small in diameter and long. Further, in the boot joint, some of the key pads close two or three separate holes that lead to different points on the bore. (This odd complication allows the maker to improve tuning of higher resonances for some notes.) Further, because of the relatively small tone holes, bassoonists can and do use cross fingerings as alternatives rather more than do other woodwind players, to vary loudness and brightness and to adjust intonation.

An open tone hole connects the bore to the air outside, whose acoustic pressure is approximately zero. But the connection is not a 'short circuit': the air in and near the tone hole has mass and requires a force to be moved. So the pressure inside the bore under a tone hole is not at zero acoustic pressure, and so the standing wave in the instrument extends a little way past the first open tone hole, particularly for long, narrow tone holes such as those on the bassoon. (There's more about this effect under Cut-off frequencies.) Closing a downstream hole extends the standing wave even further and so increases the effective length of the instrument for that fingering, which makes the resonant frequencies lower and the pitch flatter.

The effect of cross fingerings is frequency dependent. The extent of the standing wave beyond an open hole increases with the frequency, especially for small holes, because it takes more force to oscillate the air in the tone hole at high frequencies. This has the effect of making the effective length of the bore increase with increasing frequency. As a result, the resonances at higher frequencies tend to become flatter than strict harmonic ratios. Because the oboe's tone holes are not very much smaller than the bore, cross fingerings have relatively little effect on the pitch in the first two registers. They have much greater effect on the bassoon.

A further effect of the disturbed harmonic ratios of the resonances for cross fingerings is that the harmonics that sound when a note is played will not 'receive much help' from resonances in the instrument. (Technically, the bore does not provide feedback for the reed at that frequency, and nor does it provide impedance matching, so less of the high harmonics are present in the reed motion and they are also less efficiently radiated as sound. See Frequency response and acoustic impedance. To be technical, there is also less of the mode locking that occurs due to the non-linear vibration of the reed.) As a result, cross fingerings in general are less loud and have darker or more mellow timbre than do the notes on either side.

We have studied cross fingerings more extensively on flutes than on other instruments, by comparing the acoustical response of baroque, classical and modern instruments. See cross fingering on flutes or download a scientific paper about cross fingering.

Other effects of the reed

An important effect of the reed concerns the fact that the bore is not a simple cone: it is a cone truncated at a comfortable diameter to take the reed, whose effective cone angle is much greater than that of the bore. This truncation affects the tuning: informally, we can think of it as making the pipe slightly like a cylinder, which stretches the frequency gap between resonances. This means that, unless compensated, it would stretch the interval between registers to over an octave. Now the geometry of the reed is a little complicated, but one contribution to the acoustic response is that it compensates for the 'missing volume' of the cone. Indeed, its volume (including an effective volume due to the flexibility of the reed blades) is comparable with that of the missing cone.

So, as well as controlling the flow of air, the reed has a passive role. When the pressure inside the reed, the blades are pushed outwards. Conversely, suction draws the reed in towards the bore. Thus deformation of the reed blades increases and decreases the reed's air volume with high or low pressure. (Techncially, we say it is a compliance in parallel with the bore.) Indeed, it behaves a bit like an extra volume of air, which could also be compressed and expanded by changing pressure in the mouthpiece. It has the effect of lowering the frequency of each resonance a little. However, soft reeds move more than hard reeds, so soft reeds lower the frequency (and thus the pitch of the note) more than do hard reeds. Further, this effect is greater on high notes than on low, so soft reeds make intervals slightly narrower. This is useful to know if you have intonation problems. However, compared with single reeds, double reeds have the complication that flattening the blades not only decreases the reed air volume (which reduces compliance) but also decreases the blade stiffness (which increases compliance). Squeezing the blades flatter and closer together reduces the volume, which on its own would raise the pitch. Which of these effects wins can depend on the reed scrape. (This is discussed in more detail under the "effect of hardness" section on the clarinet page.) The effect of reed shape is important and complicated. However, the flat blade is stiffer (less easy to bend), which tends to raise the pitch. Reed mechanics is a very important topic and needs more explanation — another time.

Cut-off frequencies

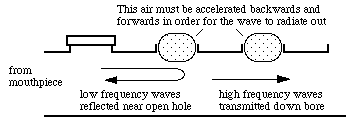
So high frequency waves are impeded by the air in the tone hole: it doesn't 'look so open' to them as it does to the waves of low frequency. Low frequency waves are reflected at the first open tone hole, higher frequency waves travel further (which can allow cross fingering) and sufficiently high frequency waves travel down the tube past the open holes. Thus an array of open tone holes acts as a high pass filter: something that lets high frequencies pass but rejects low frequencies. (See filter examples.) The cutoff frequency is roughly 1500 Hz* for the oboe and 600 Hz* for the bassoon. In the sound spectra of most low notes, the strength of harmonics falls off above this frequency. These cutoff frequencies correspond roughly to the highest pitches in the standard repertoire (though modern pieces go higher). So for the very high notes, the tone holes farthest from the reed can have a large effect on the pitch because the standing wave penetrates a long way down the bore. (As noted above, some of the bassoon's tone holes are rather long, particularly in the wing of the tenor joint and at the bottom of the boot.)

* These are very approximate values and vary considerably over the range of the instrument. Also the cutoff frequency has risen over the centuries, especially on instruments influenced by Boehm. This is a subtle topic area: see cutoff frequencies. In general, however, smaller-diameter and longer tone holes are less good at radiating high frequencies and so make for a darker timbre. This is one reason why modern instruments sound brighter than baroque. Here is a scientific paper where we compare this effect in baroque, classical and modern flutes.

Effect of the bell. A flaring bell like that of the oboe 'helps' the sound waves in the bore to radiate out into the air. (Incidentally, the presence of a large, effective bell is what makes brass instruments loud: try playing a trombone with the tuning slide taken off.) More sound radiated means less sound reflected, so the standing waves are weaker. However, this effect is only strong for high frequency: as the frequency increases over this range, the resonances are more weakened by the bell at high frequency than at low. This is because the bell is much smaller than the wavelengths of the low frequency waves, and so is less effective at radiating these waves. So we expect the oboe bell to make the timbre brighter. Doing the experiment will tell you that the effect is not huge. The cor anglais bell has only a modest effect on the timbre and the bassoon 'bell' very little.

The effect of an oboe bell is that of a high pass filter. We could say that this is rather like the cut-off frequency effect of a series of open tone holes. In fact, one purpose of the instrument's bell chiefly is to provide a high pass filter for the lowest few notes, so that they have a cut-off frequency and so behave more similarly to the notes produced with several tone holes open. As far as fundamental frequencies go, the bell is really only important to the lowest notes. However, it is important to the high harmonics of most notes.

The bell of the bassoon is the name of the last joint, which doesn't have a widening flare like oboe, clarinet or saxophone.

Notes at the very bottom of the range are difficult to play softly. We saw in How the reed and pipe work together that the higher harmonics of the reed motion could be 'helped' by resonances of the bore. When you play loudly, you generate proportionally more power in the higher harmonics (this is due to increasingly non-linear motion of the reed). So the lowest notes are not so difficult to play loudly, where the strong, high harmonics of the reed are supported by resonances of the bore, compared with soft notes, where you are relying on just the fundamental resonance. (Note, however, that the lowest notes are also most affected by leaks, for two reasons: first, they involve more keys closing and so more opportunity for leaks. Second, low frequencies have more time to accelerate air through leaks. So if the low notes are very hard to play, check for leaks.)

Vocal tract effects

More to come

This is a draft document and I'll extend and improve it as time permits. Our Introduction to saxophone acoustics has rather more detail about a conical bore interacting with a reed, because we have studied that instrument in detail.

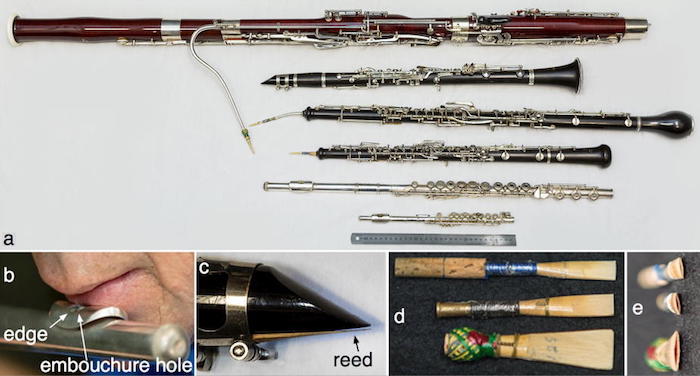
This photo shows the common orchestral woodwinds in ascending order of pitch. The double reeds are the bassoon (top), cor anglais (third) and oboe (fourth). (d) and (e) show their double reeds (oboe at the top). (Figure from The acoustics of woodwind musical instruments. Click to enlarge.)