Cutoff frequencies and crossfingering in woodwinds

Cut-off frequencies

In a very simple model of a woodwind instrument, one could say that a tone hole opens the bore up to the outside air, and so it shortens the effective length of the tube. Open more holes upstream and and the pipe becomes shorter and plays higher notes – usually. At low frequencies, and usually in the low register of the instrument, this is a reasonable approximation: the wave is reflected at or near this point because the hole provides what we might call an acoustical 'short circuit' to the outside air: we fix the air pressure at atmospheric and so make a pressure node at that point. (See Pipes and harmonics for an introduction to resonances in wind instruments.)

For high frequencies, however, it is more complicated. The air in and near the tone hole has mass. For a sound wave to pass through the tone hole it has to accelerate this mass, and the required acceleration (all else equal) increases as the square of the frequency: for a high frequency wave there is little time in half a cycle to get it moving.

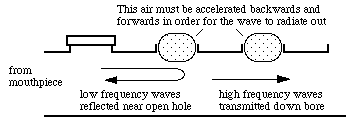
sketch: inertance of air in open tone holes

So high frequency waves are impeded by the air in the tone hole: it doesn't 'look so open' to them as it does to the waves of low frequency. Low frequency waves are reflected at the first open tone hole, higher frequency waves travel further (which can allow crossfingering) and sufficiently high frequency waves travel down the tube past the open holes. Thus an array of open tone holes acts as a high pass filter: it lets high frequencies pass but rejects low frequencies. (See filter examples.)

The cut-off frequency, f_c, depends on the geometry of the instrument in a quite complicated way. However, there is an approximate and simple equation that estimates it:

^½

where b is the radius of a typical tonehole, a the radius of the bore, v the speed of sound, s is half the typical spacing between tone holes and t the typical effective length of the tone hole, including end effects. Arthur Benade derived this for 'continuous' tone holes in 1976 (Fundamentals of Musical Acoustics Oxford). We derive it for discrete tone holes in an appendix to this paper.

This equation tells you that a baroque instrument, with small holes (small b) that are far apart (large s) will have a lower f_c than a modern one. This means that the open tone hole stops being a 'short circuit' at lower frequency. So the effective length for resonances near or above f_c is longer than for the first one or two. This puts higher resonances out of tune, which means that they don't 'assist' the higher harmonics so well, and so the instrument sounds darker than its modern offspring.

Three regimes of frequency

Let's identify three regimes: a broad regime below the cut-off frequency (f < f_c), a narrower regime of less than an octave or so (f ~ f_c) and a broad regime above the cut-off frequency (f > f_c). Before we illustrate these with measurements, let's see what the physics tells us.

For low frequencies (f < f_c), the first open tone hole is approximately a short circuit. So the bore has approximately the same effective length for all frequencies and so the bore resonances are approximately harmonic and so approximately equally spaced in frequency. Importantly, a significant of the output power is radiated from the first open tone hole.

Near the cut-off frequency (f ~ f_c), the standing wave extends somewhat beyond the first open hole, and the extent depends on frequency. Consequently, the resonance frequencies follow no simple pattern.

For high frequencies (f > f_c), the mass of the air in each open tone hole effectively seals the tone hole, so the standing wave extends all the way to the end of the instrument. In this regime, the effective length of the bore is that of the whole bore and so the frequencies of resonance become approximately equally spaced again, but with a narrower spacing than in the low frequency regime. Above f_c, a large fraction of the output sound is radiated from the bell.

Effects of cut-off frequency on flutes, clarinets and saxophones

We shall now look at some acoustic impedance spectra. (This impedance spectrum, written either Z or Z(f), may be thought of as the 'acoustic response' of the instrument. For an introduction, see 'What is an impedance spectrum?') We have data bases of impedance spectra for clarinet, saxophone and flutes from the baroque, classical and modern era.

Clarinet. The next figure shows the impedance spectrum for the note written G4 (sounding F4), the 'all fingers off' note. You can see a strong peak at about 350 Hz, corresponding to the resonance that will help the reed vibrate at that frequency and play the note. The instrument has a roughly cylindrical bore, so the next resonance that will drive the reed is at a frequency about three times higher. This fingering will play D6 (three times the frequency of G4), but not easily: it's easier with the register key. If there were no cut-off frequency, we'd also expect to see peaks at 5, 7, 9 etc times 350 Hz. But we don't.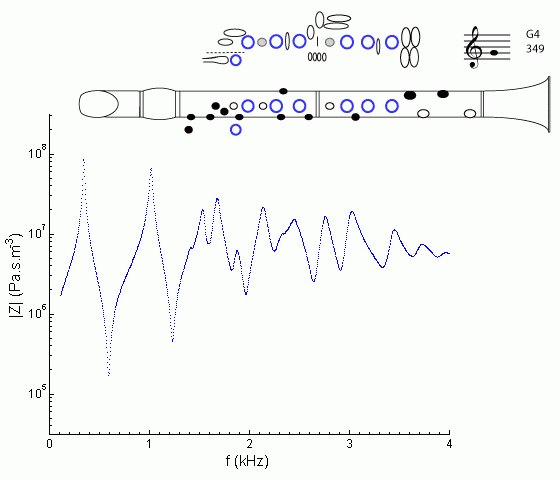

The cut-off frequency for a clarinet is about 1.5 kHz. For a range (f ~ f_c) from about 1.4 to 2.4 kHz, the impedance spectrum is irregular, as explained above. However, above this range (f > f_c) the peaks become relatively regular again. They are much more closely spaced, because now the standing waves occupy nearly the whole bore.

Notice that the peaks become weaker at high frequencies. There are two main reasons. First, at high frequencies, there are greater visco-thermal losses at the walls of the bore. Second, the bell radiates high frequencies more efficiently. (More detail here.) The cut-off frequency complicates things a little, but you'll notice that they have roughly the same magnitude and frequency of those at high frequency in the impedance spectrum for the lowest note E3.

Saxophone. Things are somewhat different for the saxophone. Because of its conical bore, it acts at high frequency like a megaphone: it's good at radiating waves rather than reflecting them. Therefore, by the time we get to the f > f_c regime, the peaks are really weak. Again, we can see that this is not an effect of the cut-off frequency, because the high frequency peaks disappear even for the lowest note, written A#3 (Impedance spectrum of A#3 here).

In the next graph, we compare saxophone and clarinet. We choose notes at the top of the first register, and we rescale the frequency axes so that the first peaks coincide. (The magnitudes are not scaled but the two peaks have rather similar magnitude.)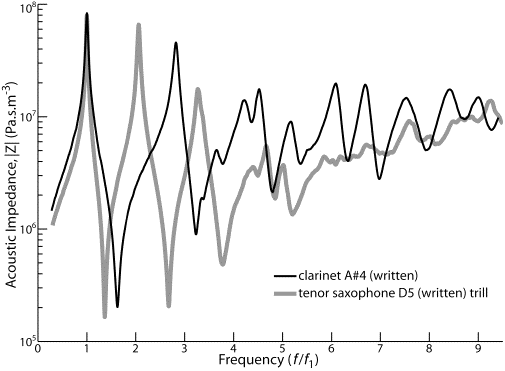

The difference between cylindrical and conical bore has several effects. We have already seen how the megaphone effect weakens high frequency resonances for the saxophone. In this graph we see the well-known effect of conical versus cylindrical bores: the frequency ratio of the first two peaks is 2:1 for the sax and 3:1 for the clarinet. This is discussed here.

Flute. Because the flute is open at the embouchure, we shall now be interested in the minima, not the maxima or impedance. (See Introduction to flute acoustics.) The cut-off frequency for the Boehm flute is a little above 2 kHz. Below this (f < f_c), the flute has the expected resonances. For example, in the graph for A4, you will see that the first four or five resonances become gradually weaker with frequency – this is due to the increasing importance of energy losses due to the 'friction' (viscous and thermal loss) between the air and the wall.

Near and a little above (f ~ f_c), the resonances are a little irregular, as discussed above. The range f > f_c has a new complication for the flute, however. The air in the blow-hole and that near the cork form a Helmholtz resonator that provides a short circuit, in parallel with the bore (explained here). So, to see the resonances corresponding to standing waves over the whole length of the bore, we need to go to frequencies above the Helmholtz short. That is shown in the next graph: the impedance spectrum for the note C#5 at the top of the first register.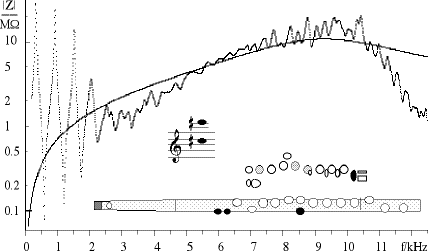

Cut-off frequency for the lowest notes? For the lowest note or two on any instrument, there is no array of open holes and so there is no cutoff frequency due to that effect. In principle, if the higher harmonics were strong enough, one would expect this to lead to a different timbre of these notes. One way to avoid this – a way that is used for the oboe and clarinet – is to supply a bell that radiates high frequencies but not low, and which has a cut-off frequency comparable with that of the tone hole array. The flute has less radiated power at high frequencies than do the oboe and clarinet, so the need for a bell to 'homogenise' the timbre is rather less. However, a bell would increase high frequency radiation, both for long and short tube notes, and the pinschofon is the name of such an instrument.

This technical paper gives measurements and analyses of cutoff frequencies and crossfingering in baroque, classical and modern flutes. The figure at the top of this page comes from that paper: it shows the acoustic impedance 'looking into' an array of open tone holes, expressed in terms of the radiation impedance from the first hole alone. For an instrument literally sawn off at the first open tone hole, the line would be horizontal for all frequencies. The modern instrument, with its large, closely spaced holes, most closely approximates this. The figure immediately above also comes from that paper.

Variation in cut-off frequency

Tone holes often vary in size (the Boehm flute is almost an exception). The distance between them must, overall, increase as one goes down the instrument. One would expect that the cut-off frequency would vary from fingering to fingering. Yes, it does, quite a bit. How important is that?

The cut-off frequency has two effects. One is on the brightness of the timbre: when one plays a note, harmonics that below f_c are 'assisted' by resonances and, when this happens, they enhance the brightness. (Which is one reason why modern instruments are brighter than their ancestors.) The second is that, at f ~ f_c, the fingerings start becoming awkward. However, the number of harmonics that fall below f_c is usually rather small (say 1 to 5), so varying the f_c by 10 or 20% has relatively little effect.

Cross fingering

On many modern woodwinds, including the Boehm flute, successive semitones are played by opening a tone hole dedicated to that purpose. There are twelve semitones in an octave, so that one needs to open twelve keys in a chromatic scale before going from say D4 in the first register to D5 in the second register – or 17 for a clarinet. Twelve holes exceeds the number of fingers on standard players, particularly when the right thumb is employed to support the instrument. Modern systems employ clutches so that one finger can close more than one hole.

Instruments in the baroque and early classical periods had few keys. Typically, they had six open holes covered by the three large fingers on each hand. Opening these holes in sequence gave the 'natural' scale of the instrument, which was D major. Writing X for closed hole and O for open, and continuing to use the flute as an example, the fingering chart for such an instrument is approximately:

F#4

C#5

classical flute

Reproduction of a classical flute by Terry McGee.

with E5 to B5 using the same fingerings as E4 to B5. (Much more detail on fingerings and how they work is given on the pages for baroque and classical flutes.)

On such instruments, cross fingerings are used to produce some of the intervening notes. In a cross fingering, further holes are closed downstream from the first open hole. For example, the fingering for F4/5 on the baroque flute is:

Compare this with the fingering for F#4/5, which is XXX XOO. For F#, the standing wave extends down the bore of the instrument past the first open hole. The extended wave is stronger in the baroque or classical instruments than in the modern flute because the holes are smaller and so the acoustic impedance between the bore and the outside field is smaller. (In the modern flute, the open hole acts more like an acoustical short circuit, so the flute behaves almost as though it were 'sawn off' at a point not far below the first open hole. So the modern flute has relatively small end corrections.) Closing the downstream hole extends the standing wave even further and so increases the effective length of the instrument for that fingering, which makes the resonant frequencies lower and the pitch flatter.

The effect of cross fingerings is frequency dependent. The extent of the standing wave beyond an open hole increases with the frequency, especially for small holes. This has the effect of making the effective length of the flute increase with increasing frequency. As a result, the impedance minima at higher frequencies tend to become flatter than strict harmonic ratios. One effect of this is that some cross fingerings cannot be used in both first and second register: the cross fingering used for G# in the first register will be too flat in the second register, or may not even play a note near G# at all. (See for example the fingerings for G#4 and G#5 on the baroque flute.)

A further effect of the disturbed harmonic ratios of the minima in impedance is that the harmonics that sound when a low note is played will not 'receive much help' from resonances in the instrument. (Technically, the bore does not provide feedback for the jet at that frequency, and nor does it provide impedance matching, so less of the high harmonics are present in the jet and they are also less efficiently radiated as sound.) As a result, the sound spectra for notes such as F4 and G#4 on the baroque flute have weaker higher harmonics, and so these notes are less loud and have darker or more mellow timbre than do the notes on either side.

We noted previously that the 'natural' scale of these instruments is D major: in D and in B minor they use no cross fingerings, so their timbre is bright. In Eb major or C minor, their timbre is dark and they play more quietly. These observations are also true of the baroque oboes, baroque (and modern) recorders, and approximately true of the baroque bassoon. I suspect that this has contributed to the different qualities associated with different keys: keys with a couple of sharps are associated with bright and relatively loud winds, whereas keys with a few flats are associated with dark and quiet winds.

Half-holing

input impedance illustrating cutoff frequencies What happens when you open a hole only part-way? On very simple woodwinds with only about six tone holes, this is sometimes necessary to produce chromatic notes. On many woodwinds, it can be used to produce a slide, though this is more awkward to achieve if the hole is covered by a key, rather than by a finger.

The graph at right (from this paper) shows a close-up of the impedance spectra of a clarinet. For the notes D5, E5, F5 and G5, the solid lines show the normal impedance peak responsible for the fundamental of those notes. Between F5 and G5 are the peaks produced by fingerings in which the RH index finger is gradually closed to go from G5 to F5. These fingerings produce notes with frequencies near their impedance peaks.

This technique alone can be used to vary the pitch. However, in many cases, the players use resonances of their vocal tracts, in cooperation with the resonance of the instrument, to achieve pitch bending and microtones. Note that the impedance peak becomes smaller as the hole becomes more nearly closed. With only a small leak, the peak can be reduced by a factor of several (note that the vertical axis is logarithmic). This makes it easier for the vocal tract resonance to control the pitch. The paper referred to above explains both techniques, including an explanation of the famous glissando in Gershwin's Rhapsody in Blue.

How does half-holing change the end effect and the impedance spectrum? If we imagined cutting off the end of the instrument, we'd have a very strong reflection, and an end effect that extends the length by about 0.6 times the radius. A large tone hole provides a reasonably strong reflection though, as explained above, the reflection is less strong for higher frequencies. A smaller tone hole provides less reflection and so proportionately more of the wave propagates further down the bore, reflecting at open holes lower down. The reflections are now out of phase, which weakens the impedance peak and makes the note easier to bend, using the vocal tract or the embouchure.

Because of the dependence of the end effect on frequency, half-holing usually has a greater effect on notes in the higher registers. Further, half-holing puts the resonances out of tune. This means that fewer resonances may 'cooperate' in producing a note, several of whose harmonics might be supported by a bore resonance in a normal note. This can make pitch bending easier.

References

The figures shown above come from these papers.

Chen, J.M., Smith J. and Wolfe, J. (2009) "Saxophone acoustics: introducing a compendium of impedance and sound spectra" Acoustics Australia, 37, 18-23.
Chen, J.M., Smith J. and Wolfe, J. (2009) "Pitch bending and glissandi on the clarinet: roles of the vocal tract and partial tone hole closure" J. Acoust. Soc. America, 126, 1511-1520.
Dickens, P., France, R., Smith,. J. and Wolfe, J. (2007) "Clarinet acoustics: introducing a compendium of impedance and sound spectra". Acoustics Australia, 35, 17-24.
Wolfe, J. and Smith, J. (2003) "Cut off frequencies and cross fingering in baroque, classical and modern flutes", J. Acoust. Soc. America, 114, 2263-2272.
Wolfe, J., Smith, J., Tann, J. and Fletcher, N.H. (2001) "Acoustic impedance of classical and modern flutes" Journal of Sound and Vibration , 243, 127-144.

The data bases of impedance spectra for clarinet, saxophone and flutes are web appendices to three of these papers.

Further information

Related questions are addressed on our FAQ in Music Acoustics.
If you found this page already too technical, try How do woodwind instruments work?.
For background on topics in acoustics (waves, frequencies, resonances etc) see Basics.

Cutoff frequencies, crossfingering and half-holing in woodwinds