What is a Sound Spectrum?

A sound spectrum displays the different frequencies present in a sound.

Most sounds are made up of a complicated mixture of vibrations. (There is an introduction to sound and vibrations in the document "How woodwind instruments work".) Perhaps you can hear the sound of the wind outside, the rumble of traffic - or perhaps you have some music playing in the background, in which case there is a mixture of high notes and low notes, and some sounds (such as drum beats and cymbal crashes) which have no clear pitch.

A sound spectrum is a representation of a sound – usually a short sample of a sound – in terms of the amount of vibration at each individual frequency. It is usually presented as a graph of either power or pressure as a function of frequency. The power or pressure is usually measured in decibels and the frequency is measured in vibrations per second (or hertz, abbreviation Hz) or thousands of vibrations per second (kilohertz, abbreviation kHz). You can think of the sound spectrum as a sound recipe: take this amount of that frequency, add this amount of that frequency etc until you have put together the whole, complicated sound.

Today, sound spectra (the plural of spectrum is spectra) are usually measured using

  • a microphone which measures the sound pressure over a certain time interval,
  • an analogue-digital converter which converts this to a series of numbers (representing the microphone voltage) as a function of time, and
  • a computer which performs a calculation upon these numbers.

Your computer probably has the hardware to do this already (a sound card). Many software packages for sound analysis or sound editing have the software that can take a short sample of a sound recording, perform the calculation to obtain a spectrum (a digital fourier transform or DFT) and display it in 'real time' (i.e. after a brief delay). If how have these, you can learn a lot about spectra by singing sustained notes (or playing notes on a musical instrument) into the microphone and looking at their spectra. If you change the loudness, the size (or amplitude) of the spectral components gets bigger. If you change the pitch, the frequency of all of the components increases. If you change a sound without changing its loudness or its pitch then you are, by definition, changing its timbre. (Timbre has a negative definition - it is the sum of all the qualities that are different in two different sounds which have the same pitch and the same loudness.) One of the things that determines the timbre is the relative size of the different spectral components. If you sing "ah" and "ee" at the same pitch and loudness, you will notice that there is a big difference between the spectra.

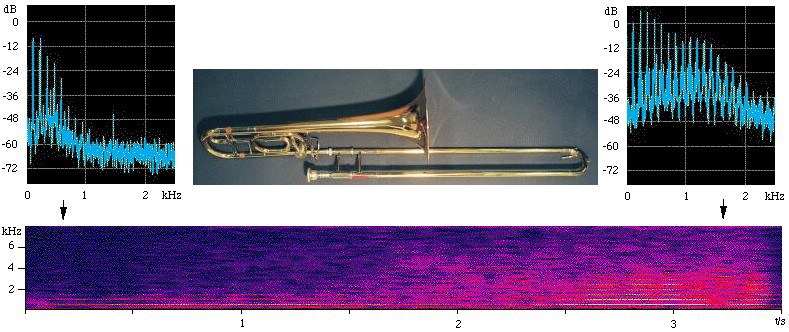
spectra and spectrogram of a crescendo

In this figure, the two upper figures are spectra, taken over the first and last 0.3 seconds of the sound file. The spectrogram (lower figure) shows time on the x axis, frequency on the vertical axis, and sound level (on a decibel scale) in false colour (blue is weak, red is strong). In the spectra, observe the harmonics, which appear as equally spaced components (vertical lines). In the spectrogram, the harmonics appear as horizontal lines. In this example, the pitch doesn't change, so the frequencies of the spectral lines are constant. However the power of every harmonic increases with time, so the sound becomes louder. The higher harmonics increase more than do the lower, which makes the timbre 'brassier' or brighter, and also makes it louder.

Spectra and harmonics

If you have tried looking at the spectrum of a musical note, or if you have looked at any of the sound spectra on our web pages then you will have noticed they have only a small number of prominent components at a special set of frequencies. Here is a sound spectrum for the note G4 played on a flute (from our site on flute acoustics), which is convenient because the pitch of this note corresponds approximately to a frequency of 400 Hz, which is round number for approximate calculations.

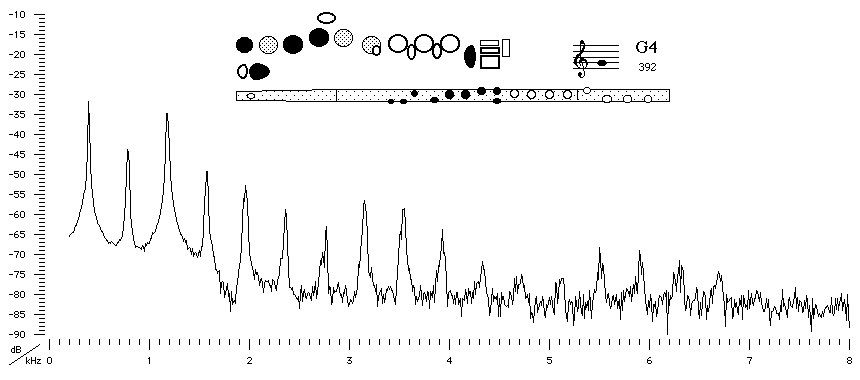
spectrum of a flute playing G4

The sound spectrum of the flute playing this note has a series of peaks at frequencies of

400 Hz   800 Hz   1200 Hz   1600 Hz   2000 Hz   2400 Hz etc,     which we can write as:

f   2f   3f   4f ... nf ... etc,

where f = 400 Hz is the fundamental frequency of vibration of the air in the flute, and where n is a whole number.

This series of frequencies is called the harmonic series whose musical importance is discussed in some detail in "The Science of Music". The individual components with frequencies nf are called the harmonics of the note.

The fundamental frequency of G4 is 400 Hz. This means that the air in the flute is vibrating with a pattern that repeats 400 times a second, or once every 1/400 seconds. This time interval - the time it takes before a vibration repeats - is called the period and it is given the symbol T. Here the frequency f = 400 cycles per second (approximately) and the period T = 1/400 second. In other words

T = 1/f.

where T is the period in seconds, and f the frequency in hertz. In acoustics, it is useful to note that this equation works too for frequency in kHz and period in ms.

If we were to look at the sound of a G4 tuning fork, we would find that it vibrates at (approximately) 400 times per second. Its vibration is particularly simple – it produces a smooth sine wave pattern in the air, and its spectrum has only one substantial peak, at (approximately) 400 Hz. You know that the flute and the tuning fork sound different: one way in which they are different is that they have a different vibration pattern and a different spectrum. So let's get back to the spectrum of the flute note and the harmonic series. This is a harmonic spectrum, which has a special property, which we'll now examine.

Consider the harmonics of the flute note at

f   2f   3f   4f ... nf ,

The periods which correspond to these spectral components are, using the equation given above:

T   T/2   T/3   T/4 ... T/n .

Consider the second harmonic with frequency 2f. In one cycle of the fundamental vibration (which takes a time T) the second harmonic has exactly enough time for two vibrations. The third harmonic has exactly enough time for three vibrations, and the nth harmonic has exactly enough time for n vibrations. Thus, at the end of the time T, all of these vibrations are 'ready' to start again, exactly in step. It follows that any combination of vibrations which have frequencies made up of the harmonic series (i.e. with f, 2f, 3f, 4f, .... nf) will repeat exactly after a time T = 1/f. The harmonic series is special because any combination of its vibrations produces a periodic or repeated vibration at the fundamental frequency f. This is shown in the example below.

Beofre we leave this example however, let's look between the harmonics. In both of the examples shown above, the spectrum is a continuous, non-zero line, so there is acoustic power at virtually all frequencies. In the case of the flute, this is the breathy or windy sound that is an important part of the characteristic sound of the instrument. In these examples, this broad band component in the spectrum is much weaker than the harmonic components. We shall concentrate below on the harmonic components, but the broad band components are important, too.

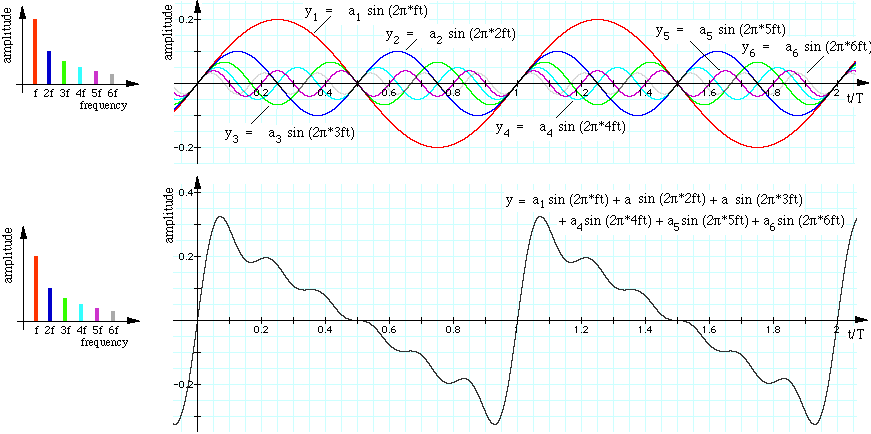
An example of an harmonic spectrum: the sawtooth wave

The graph below shows the first six harmonics of a sawtooth wave, named for its shape. On the left is the (magnitude) spectrum, the amplitudes of the different harmonics that we are going to add. The upper right figure shows six sine waves, with frequency f, 2f, 3f etc. The lower figure shows their sum. (As more and more components are added, the figure more closely approaches the sawtooth wave with its sharp points.)

The first six harmonics of a sawtooth wave, sounded one at a time.

When you hear a complex spectrum built up one harmonic at a time, you can clearly hear the individual 'notes' in the 'chord'. You may also be able to hear the harmonics in a sustained note. However, if you hear a series of notes, each containing several harmonics, you hear each successive note as an entity, and it is much more difficult to distinguish the individual harmonics. This is demonstrated in the example below. The first note of the melody is synthesised sequentially, using the harmonics in the example given above.

Sequential synthesis using the first six harmonics, then a melody using that spectrum.

The spectrum can be regarded as like a recipe for making up the whole waveform: take this much (a1) of frequency f, this much (a2) of frequency 2f,... plus thus much (Aan) of frequency nf,.... , and add them together. (For a sound wave, the vertical axis on all these graphs could be sound pressure p.) (If you are an organist, you will be familiar with this principle. Adding those harmonics sounds much like coupling ranks of organ pipes. If you were to couple 16', 8', 5.33', 4',3.2' and 2.67' flutes, then play a melody, you would get much the same effect.) In this example, we have added all the components in phase (starting from zero at the same time). This is a special case and, in general, the phase constant at each frequency would make up a part of the spectrum, too.

The result we have just shown is (roughly speaking) one side of a theorem proved by the French mathematician Fourier. He showed that it is also true in the other direction: a repeated vibration with fundamental frequency f can always be made up of a combination of vibrations with the harmonic frequencies f, 2f, 3f, 4f, .... nf).

This other direction is difficult to demonstrate without mathematics, though you will see that the sound spectra for the flute notes have harmonic spectra. You may nevertheless notice some strange behaviour for some of the higher notes.

  • First, we only show the spectra up to 4 kHz for low notes and 8 kHz for high ones. Therefore, once the notes get to the top half octave of the flute (C7 and above), the fourth and higher harmonics are already off scale.
  • Second, you will see some "sub-harmonics" in a few notes. Look for example at the sound spectrum of the note E6 played without the "split E" mechanism. The strong peak at approximately 1320 Hz is the fundamental for E6, and you can see the strong peaks for the 2 times, 3 times, 4 times and 5 times this frequency. All as expected, but you will also notice some weaker peaks at 440 Hz and 880 Hz, corresponding to the notes A4 and A5.

    So why don't we hear this note as A4, with a particularly strong 3rd harmonic? Well, remember that the vertical scale is in decibels. The two subharmonics are 41 and 45 dB below the component at 1320 Hz so the subharmonics have less than 0.01% of the power of the fundamental. (Further, as the frequency falls below 1000 Hz, the sensitivity of the human ear decreases substantially with frequency over the range below 1000 Hz, which also diminishes the contribution we might hear from the low frequency components.)

    If you look at the spectrum for the flute impedance for this fingering (especially for the flute without a split E mechanism) you will see why: the flute has impedance minima at 440, 880, 1320 and several other frequencies, and so it is difficult to put acoustic power into the flute without exciting these other vibrations, at least to a little. (This creates other problems for flutists, too. See Why is Acoustic Impedance Important?)

    So why don't we hear A4? Well, remember that the vertical scale is in decibels. The A4 is 40 dB below the component at 1320 Hz and so has about 0.01% of the power of the fundamental. (Further, the sensitivity of the human ear increases substantially with frequency over the range below 1000 Hz, which also diminishes the contribution we might hear from the low frequency components.)

  • Third, you will notice that the sound spectra of the notes in the top range (see e.g. E7) of the flute contain some small components that are not even in the harmonic series. These notes are not easy to play (observe the weakness of the relevant minimum in the impedance spectrum), and can only be played loudly (if at all). The sound of the blast of air from the player's mouth (try blowing very hard with your mouth almost entirely shut) contributes measurably to the spectrum in these cases.
  • The multiphonic spectra (see D5 with F5) look a little like two or more sets of spectra at once. i.e. they look at bit like

    f, 2f, 3f etc, and also

    g, 2g, 3g etc,

    where f and g are the fundamental frequencies of the notes in the multiphonic chord. But it is a bit more complicated than this, and you will notice some other small but non-negligible components at other frequencies, including e.g. 2g-f.

Some special cases. A cylindrical pipe, closed at one end, resonates at only the odd harmonics of its fundamental. Consequently a closed organ pipe has strong odd harmonics (fundamental, 3rd, 5th etc) and weak even harmonics (2nd, 4th etc). This effect is discussed in "pipes and harmonics" and "flutes vs clarinets.

The same is true of the lowest register of a clarinet (the chalumeau register), but not of higher registers, for reasons to do with the tone holes. This is discussed in "clarinet acoustics".

Finally, an important caveat. Introductory physics text books sometimes give the impression that the spectrum is the dominant contribution to the timbre of an instrument, and that certain spectra are characteristic of particular instruments. With the exception of the closed pipes mentioned above, this is very misleading. Some very general or vague comments can be made about the spectra of different instruments, but it is not possible to look at a harmonic spectrum and say what instrument it comes from. Further, it is quite possible for similar spectra to be produced by instruments that don't sound very similar. For instance, if one were to take a note played by a violin and filter it so that its spectrum were identical to a given spectrum for a trumpet playing the same note, the filtered violin note would still sound like a violin, not like a trumpet.

Here are some general statements about spectra:

  • bowed strings and winds have harmonic spectra
  • plucked strings have almost harmonic spectra
  • tuned percusion have approximately harmonic spectra
  • untuned percusion have nonharmonic spectra
  • the low register of the clarinet has mainly odd harmonics
  • bowed strings have harmonics that decrease relatively slowly with frequency
  • brass instruments often have spectra whose harmonics have amplitudes that increase with frequency and then decrease.
To say anything that is much more specific than that is misleading.

[Basics | Research | Publications | Flutes | Clarinet | Saxophone | Brass | Didjeridu | Guitar | Violin | Voice | Cochlear ]
[ People | Contact Us | Home ]

© Joe Wolfe / J.Wolfe@unsw.edu.au
phone 61-2-9385 4954 (UT + 10, +11 Oct-Mar)
Joe's music site

Happy birthday, theory of relativity!

As of June 2005, relativity is 100 years old. Our contribution is Einstein Light: relativity in brief... or in detail. It explains the key ideas in a short multimedia presentation, which is supported by links to broader and deeper explanations.
Music Acoustics Homepage What is a decibel? Didjeridu acoustics