Loudness and Spectra

Site map | Contact Us

Loudness and spectra

Loudness depends not only on the amplitude of a wave, but also on its frequency and spectrum. This is mainly because our ears are not equally sensitive to all frequencies (for details, see What is a a decibel?)

In the illustration below (taken from our page on brass acoustics), the two upper figures are spectra that were taken over the first and last 0.3 seconds of the sound file.

The spectrogram (lower figure) shows time on the x axis, frequency on the vertical axis, and sound level (on a decibel scale) in false colour (blue is weak, red is strong). In the spectra, note the harmonics, which appear as equally spaced components (vertical lines). In the spectrogram, the harmonics appear as horizontal lines - they have constant frequency. The power of each harmonic increases with time, so the sound becomes louder. The higher harmonics increase more than do the lower, which makes the timbre 'brassier' or brighter, and also makes it louder. The fundamental increases by only 8 dB, but the ninth and some higher harmonics--in the sensitive range of your ear--increase by more than 45 dB.

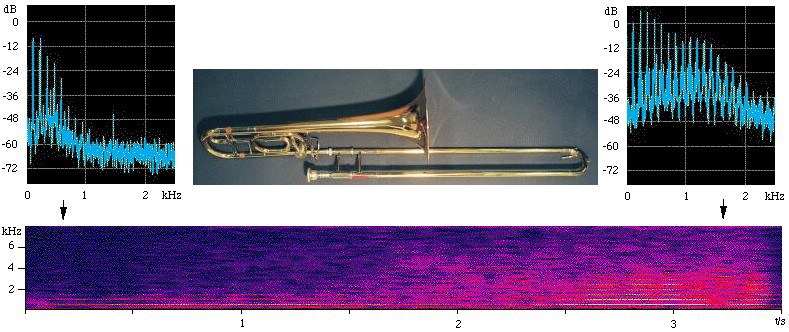
spectra and spectrogram of a crescendo

The higher harmonics make the note sound louder partly because they add extra power to the sound wave, but also because our ears become more sensitive as the frequency increases with increasing frequency (at least up to about a kHz). The greater level of high harmonics also makes the forte note sound richer in timbre.

So adding higher harmonics makes notes sound louder. The reverse is usually true: when one plays more loudly, one generates more high harmonics. This is because the instruments become more nonlinear with increasing amplitude of vibration. This is discussed, for example, in this section of our clarinet page.

The flute provides a particularly interesting example. If you look at the spectra for the flute note C4 played at different dynamic levels, you will notice that

Most musical instruments and many other oscillating systems show similar behaviour---as the vibration becomes larger, more harmonics appear. We can easily tell the difference between, for example, someone shouting and someone speaking softly into a loud public address system. For small vibrations, the relationship between displacement and restoring force is linear---in the case of a spring, the proportionality between the two is called Hooke's law. As the amplitude of vibration becomes larger, the linear approximation is a successively poorer representation of the curvilinear relation between force and displacement. A linear relationship gives a linear differential equation whose solution is a simple sine wave. As the relationship becomes more non-linear, the solution looks like a distorted sine wave - usually the peaks level off. This wave is still periodic, so it has a harmonic spectrum (see sound spectrum) but the more complicated wave shape has successively more power in the high harmonics.

Compared to some other instruments (e.g. clarinet, saxophone and violin), the flute has a relatively small dynamic range. Players take advantage of the change in timbre to make louder notes in the low register: they use a pure tone for piano and a rich "buzzy" tone for forte. They also tend to use more vibrato on loud notes, because a changing note is more noticeable than a steady one. Listen to the sound clips of Geoffrey Collins playing C4 at three different dynamic levels. Notice the different timbre and the different use of vibrato. Notice, too, how he uses varies the amount of vibrato during the note to help "shape" it. Compare this with the sound clips of Catherine McCorkill playing E3.