
| |
||
| |
||
 |
||
| |
|
|
|
|
In the example above, it's an ugly surprise, because 229 Hz is not in your chord: it's 66 cents or two thirds of a semitone sharper than A3 (220 Hz) – it's closer to A# and than A. The natural reaction is to play the C# a little flatter: if you pull it from 1109 down to 1100 Hz, the Tartini tone falls to 220 Hz, so it's now in tune and no longer annoys you. The effect is spectacular: you've lowered your note by 9 Hz, which is 14 cents at 1100 Hz, so the Tartini tone has come down by 9 Hz, but at 220 Hz, a 9 Hz change is 67 cents—two thirds of a semitone.
You've pushed your interloping note into tune; even better, your A-C# chord now sounds particularly pure. This slightly narrower third is a pure third, or a third in just intonation: it has a frequency ratio of 1100/880 or 5/4. This ratio has a long history in harmony and temperament. It has some physical importance, too.
Suppose two cellists tune their A strings in exact unison at 220 Hz. One of them then plays what string players call a 'natural harmonic': touching the string very lightly, but not stopping it. If she touches the string (with art and cunning) at a position 1/n along its length, n a whole number, then it can vibrate in n loops, with (n−1) stationary points along its length, not counting nut and bridge. The most common one is the touch fourth, illustrated below.
In fact, when any bowed string or wind instrument plays A2, it will usually produce a sound spectrum that contains a collection of harmonics, including the fourth and fifth, at 880 and 1100 Hz. So, in this sense, our ears are very accustomed to just thirds.
Equal temperament (ET) is one compromise: it uses equal thirds and equal semitones (whose ratios are respectively 21/3 (major), 21/4 (minor) and 21/12). The intonation problems are thus spread equally over all intervals, one of whose consequences is that the only difference in the sound of different keys is the difference in pitch. So Db major sounds a semitone higher than C major, but the intervals have the same ratios. (Some composers complain about this: they want Db to be sadder than C. Experienced amateur players like me, however, can assure them that the sadness will be provided by the extra wrong notes that gratuitous writing in five flats is likely to produce!)
Equal temperament does, however, produce the impure thirds and out-of-tune Tartini tones like the one we discussed above.
So why does this vexed problem for harpsichordists not affect pianists? There are two reasons. First, harpsichordists can minimise the problem by putting the pieces in flat keys before the interval, during which they retune for the sharp key pieces in the second half. For a piano, this is impossible, so there's no point worrying about it. The second, more important reason has to do with the triplets or duplets of strings on the piano.
Good piano tuners tune the strings in a duplet or triplet to slightly different frequencies. This has three important effects. First, it means that, soon after being struck, the strings are not vibrating in phase: while one string is going down, its neighbours in the triplet are going up. This reduces the vibrational force on the bridge, which in turn means that the strings lose their energy less quickly. This gives the piano its long sustain after-sound. Second, the slight differences give the sound an interesting liveliness, somewhat like the chorus effect that distinguishes the sound of a violin section from that of one violin. Third, it makes it impossible to distinguish Tartini tones, and reduces the unpleasantness of impure intervals.
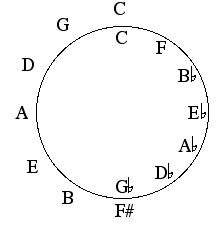
Fourths, fifths and the 'circle'At first, it seems that fourths and fifths don't cause the same problems. A pure fifth has the ratio 3/2 = 1.500 and a fourth 4/3 = 1.333, while the ET fifth and fourth are 27/12 = 1.498 and 25/12 = 1.335. So the differences are tiny. The trouble comes if we stack them up. Nearly every musician spends some time, first in wonder then in worry, on discovering the circle of fourths (or circle of fifths). Play four ascending notes in a major scale, say C-F. Then another: F-Bb. Continuing thus, and setting Gb = F#, we have C-F-Bb-Eb-Ab-Db-Gb(=F#)-B-E-A-D-G-C. On a piano, Gb = F# so, after 12 fourths, we have covered five octaves and come back 'home' to C — hence the circle, which is shown at right. Twelve pure fourths (4/3)12 = 31.6. On a keyboard, where Cb = B, 12 fourths is five octaves, which is 25 = 32.0. Out by 1.3% or a quarter of a semitone, called the Pythagorean comma — it's not a new problem! Not that we stack them up like this often, but see below. |
|
If one retains perfect fourths and fifths, the fourths make a spiral (or even a helix), as shown in the figure at right, rather than a circle. |
The Tartini tone is most easily heard between two notes that are fairly loud (i.e. close to you) and high. To demonstrate, I like to use two descant recorders, which I can blow simultaneously, fingering G on one (TXXXOOO), then successively B, C and D on the other (TXOOOOO, TOXOOOO, OXOOOO). (These fingerings produce C then E, F and G on an alto recorder.) Once you recognise Tartini tones, they can be helpful in chamber music for tuning thirds (as in the example above) and also fourths and fifths.
In the Tartini tone examples discussed above, two tones of frequencies f1 and f2 produce the sensation of a pitch with frequency f2−f1 even though there is no sound wave with that frequency (and nothing outside your head is vibrating with frequency f2−f1). Two signals with frequencies f1 and f2 can however produce a signal with frequency f2−f1 (among others) if they are input to a nonlinear system, by a process called heterodyning or nonlinear superposition. (f2−f1 is a heterodyne frequency, as is f2+f1, 2f1−f2, and others.) The details are interesting and I introduce them here and give some examples.
Now a sounding woodwind reed or a brass instrument player's lips are examples of (strongly) non-linear systems. So playing the note with f1 and singing the note with f2 can produce a note with frequency f2−f1. This heterodyne tone is often much stronger than a Tartini tone. Further, in this case there really is air vibration at frequency f2−f1, as one can see in the spectrum of its microphone output. In my nomenclature, this distinguishes heterodyne components from pure Tartini tones, for which there is no acoustic signal at f2−f1.
Heterodyne production is used to produce notes below the range of an instrument. If you play a note with f1 and sing the note a fifth higher (f2 = 3f1/2) then the difference frequency f2−f1= f1/2: you hear the note one octave below the instrument's note. To go two octaves below, sing a just major third above (f2 = 5f1/4). This technique is very important (and very impressive) on the didjeridu.
A bowed string is also a nonlinear system. So, when two notes are played as double stops on a violin, heterodyne components are produced. If the two notes were played on two violins, the (weak) Tartini tone would be heard at f2−f1, but there would be no acoustic signal at this frequency. Played as a double stop on one violin, the (strong) heterodyne component at f2−f1 is not only heard, but is present in the sound signal, because the same bow and its stick-slip action is coupled to the motion of both strings. The heterodyne signal in this case is not an illusion, in the sense used above.
Because (pure) Tartini tones are weak, they are best heard between reasonably high notes, so that the Tartini tone falls in a range where the ear is sensitive. Heterodyne tones are strong and make impressive bass notes on didjeridu, saxophone or brass instruments.
* I use the word 'illusion' to stress that, for example, when you hear pure tones at 200 Hz and 300 Hz together producing a Tartini tone with pitch corresponding to a pure tone at 100 Hz, there is no acoustic power at 100 Hz. It is true that three cycles of 300 Hz takes the same time as two cycles of 200 Hz, so the pattern repeats every 10 ms. What is interesting is that, from those two pure tones, your ear (or suitable software or hardware) can create the impression of a tone at 100 Hz. In a nice analogy that also involves non-existent frequency components, it's interesting to refer to the colour yellow, as produced on a computer monitor or television, as a visual illusion, in the sense that no yellow light is ever emitted from those screens. See this site for details.) If you would prefer to call a Tartini tone a real note (or computer yellow a real colour), that's fine.
|
|
|
|