
| |
||
| |
||
 |
||
| |
|
|
|
|
How do we make musical sounds? To make a sound, we need something that vibrates. If we want to make musical notes, you usually need the vibration to have a nearly constant frequency: that means stable pitch. We also want a frequency that can be easily controlled by the player. In electronic instruments this is done with electric circuits or with clocks and memories. In non-electronic instruments, the stable, controlled vibration is usually produced by a standing wave. Here we discuss the way strings work. This is also a useful introduction for studying wind instruments, because vibrating strings are easier to visualise than the vibration of the air in wind instruments. Geometrically, both are less complicated than the vibrations of the bars and skins of the percussion family. For the basic physics of standing waves, see our multimedia tutorial.
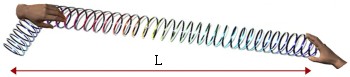 The strings in the violin, piano and so on are stretched
tightly and vibrate so fast that it is impossible to see what
is going on. If you can find a long spring (a toy known as a 'slinky' works well) or several metres of flexible rubber
hose you can try a few fun experiments which will make it
easy to understand how strings work. (Soft rubber is good
for this, garden hoses are not really flexible enough.)
First hold or clamp one end and then, holding the other end
still in one hand, stretch it a little (not too much, a little
sag won't hurt). Now pull it aside with the other hand to
make a kink, and then let it go. (This, in slow motion, is
what happens when you pluck a string.) You will probably see
that the kink travels down the "string", and then
it comes back to you. It will suddenly tug your hand sideways
but, if you are holding it firmly, it will reflect again.
The strings in the violin, piano and so on are stretched
tightly and vibrate so fast that it is impossible to see what
is going on. If you can find a long spring (a toy known as a 'slinky' works well) or several metres of flexible rubber
hose you can try a few fun experiments which will make it
easy to understand how strings work. (Soft rubber is good
for this, garden hoses are not really flexible enough.)
First hold or clamp one end and then, holding the other end
still in one hand, stretch it a little (not too much, a little
sag won't hurt). Now pull it aside with the other hand to
make a kink, and then let it go. (This, in slow motion, is
what happens when you pluck a string.) You will probably see
that the kink travels down the "string", and then
it comes back to you. It will suddenly tug your hand sideways
but, if you are holding it firmly, it will reflect again.
First you will notice that the speed of the wave in the string increases if you stretch it more tightly. This is useful for tuning instruments — but we're getting ahead of ourselves. It also depends on the "weight" of the string — it travels more slowly in a thick, heavy string than in a light string of the same length under the same tension. (Strictly, it is the ratio of tension to mass per unit length that determines speed, as we'll see below.) Next let's have a close look at the reflection at the fixed end. You'll notice that if you initially pull the string to the left, the kink that travels away from you is to the left, but that it comes back as a kink to the right — the reflection is inverted. This effect is important not only in string instruments, but in winds and percussion as well. When a wave encounters a boundary with something that won't move or change (or that doesn't change easily), the reflection is inverted. (The fact that it is inverted gives zero displacement at the end. However, reflection with any phase change will give a standing wave.) |
A sketch of the reflection of travelling kinks caused by plucking a string. At the instants represented by (e) and (m), the string is straight so it has lost the potential energy associated with pulling it sideways, but it has a maximum kinetic energy. Note that, at the reflections, the phase of the kink is changed by 180°: from up to down or vice versa. Notice also how the kinks 'pass through' each other when they meet in the middle.
Why is the reflection inverted? Well, if we assume that it is clamped or tied to a fixed object, the point of reflection didn't actually move. But look at the motion of the string by comparing the different times represented in the left hand sketches. Note that the string behind the kink is moving back towards the undisturbed position (down in the sketch). As the kink approaches the end, it becomes smaller and, when it reaches the immovable end, there is no kink at all - the string is straight for an instant. But the string still has its downwards momentum, and that carries it past the position of rest, and produces a kink on the other side, which then moves back in the other direction. (The motion of waves in strings is described in more detail in Travelling Waves, which has film clips and animations. On this page, however, we'll concentrate on the musical implications. )
As mentioned above, this motion is only observed immediately after the pluck. As the high frequency components lose energy, the sharp kinks disappear and the shape gradually approaches that of the fundamental mode of vibraiton, which we discuss below.
A sketch of the reflection of travelling kinks caused by bowing a string. See the animation and an explanation of the bow-string interaction in Bows and strings
| The animation shows the interaction of two waves, with equal frequency and magnitude, travelling in opposite directions: blue to the right, green to the left. The red line is their sum: the red wave is what happens when the two travelling waves add together (superpose is the technical term). By stopping the animation, you can check that the red wave really is the sum of the two interacting travelling waves. The figure at right is the same diagram represented as a time sequence - time increases from top to bottom. You could think of it as representing a series of photographs of the waves, taken very quickly. The red wave is what we would actually see in a such photographs. Suppose that the right hand limit is an immoveable wall. As discussed above, the wave is inverted on reflection so, in each "photograph", the blue plus green adds up to zero on the right hand boundary. The reflected (green) wave has the same frequency and amplitude but is travelling in the opposite direction. At the fixed end they add to give no motion - zero displacement: after all it is this condition of immobility which causes the inverted reflection. But if you look at the red line in the animation or the diagram (the sum of the two waves) you'll see that there are other points where the string never moves! They occur half a wavelength apart. These motionless points are called nodes of the vibration, and they play an important role in nearly all of the instrument families. Halfway between the nodes are antinodes: points of maximum motion. But note that these peaks are not travelling along the string: the combination of these two waves travelling in opposite directions produces a standing wave. This is shown in the animation and the figure. Note the positions (nodes) where the two travelling waves always cancel out, and the others (antinodes) where they add to give an oscillation with maximum amplitude. You could think of this diagram as a representation (not to scale) of the sixth harmonic on a string whose length is the width of the diagram. This brings us to the next topic. |
The string on a musical instrument is (almost) fixed at both ends, so any vibration of the string must have nodes at each end. Now that limits the possible vibrations. For instance, the string with length L could have a standing wave with wavelength twice as long as the string (wavelength λ = 2L) as shown in the first sketch in the next series. This gives a node at either end and an antinode in the middle.
This is one of the modes of vibration of the string ("mode of vibration" just means style or way of vibrating). What other modes are allowed on a string fixed at both ends? Several standing waves are indicated in the next sketch.
A sketch of the first four modes of vibration of an idealised* stretched string with a fixed length L. The vertical axis has been exaggerated.
Let's work out the relationships among the frequencies of these modes. For a wave, the frequency is the ratio of the speed of the wave to the length of the wave: f = v/λ. Compared with the string length L, you can see that these waves have lengths 2L, L, 2L/3, L/2. We could write this as 2L/n, where n is the number of the harmonic.
The fundamental or first mode has frequency f1 = v/λ1
= v/2L,
The second harmonic has frequency f2 = v/λ2
= 2v/2L = 2f1
The third harmonic has frequency f3 = v/λ3
= 3v/2L = 3f1,
The fourth harmonic has frequency f4 = v/λ4
= 4v/2L = 4f1, and, to generalise,
The nth harmonic has frequency fn = v/λn = nv/2L = nf1.
All waves in a string travel with the same speed, so these waves with different wavelengths have different frequencies as shown. The mode with the lowest frequency (f1) is called the fundamental. Note that the nth mode has frequency n times that of the fundamental. All of the modes (and the sounds they produce) are called the harmonics of the string. The frequencies f, 2f, 3f, 4f etc are called the harmonic series. This series will be familiar to most musicians, particularly to buglers and players of natural horns. For example, consider the fundamental of the note C3 (or viola C, or the C below middle C, having a nominal frequency of 131 Hz: see this link for a table). C3 has harmonics with the pitches shown in the next figure. These pitches have been approximated to the nearest quarter tone. The octaves are exactly octaves, but all other intervals are at least slightly different from the intervals in the equal tempered scale.
| The figure shows the musical notation for the first
twelve harmonics on a C3 string. When you play the sound file, listen
carefully to the pitch. The seventh and eleventh harmonics fall
about halfway between notes on the equal tempered scale, and so
have been notated with half sharps.
|
|
(* If you have just done this experiment, you may have noticed some peculiarities. The twelfth fret, which is used to produce the octave, is less than half way along the length of the string, and so the position where you touch the string to produce the 2nd harmonic – halfway along the string – is not directly above the octave fret. I said "idealised" string above, meaning a string that is completely flexible and so can bend easily at either end. In practice, strings have a finite bending stiffness and so their effective length (the "L" that should be used in the above formulae) is a little less than their physical length. This is one of the reasons why larger strings usually have a winding over a thin core, why the bridge is usually at an angle that gives the fatter strings longer lengths and why the (solid) G string on a classical guitar has poor tuning on the higher frets. There is also an effect due to the extra stretching of a string when it is pushed down to the fingerboard, an effect which is considerable on steel strings.)
An exercise for guitarists. On a guitar tuned in the usual way, the B string and high E string are approximately tuned to the 3rd and 4th harmonics of the low E string. If you pluck the low E string anywhere except one third of the way along, the B string should start to vibrate, driven by the vibrations in the bridge from the harmonic of the first string. If you pluck the low E string anywhere except one quarter of the way along, the top E string should be driven similarly.
![]()
![]() Open A string played normally, then the touch fourth on this string
(4th harmonic)
Open A string played normally, then the touch fourth on this string
(4th harmonic)
The pitch of a note is determined by how rapidly the string vibrates. This depends on four things:
We can put all of this in a simple expression. If the vibrating part of the string has a length L and a mass M, if the tension in the string is F and if you play the nth harmonic, then the resulting frequency is
Let's see where this expression comes from. The wave travels a distance λ in one period T of the vibration, so v = λ/T. The frequency f = 1/T = v/λ. So f = v/λ. We also saw that, for the fundamental frequency f1, the string length is λ/2, so f1 = v/2L. The wave speed is determined by the string tension F and the mass per unit lenght or linear density μ = M/L, v = (F/μ)1/2 = (FL/M)1/2. So f1 = ½(F/LM)1/2. Multiplying both sides by n gives the frequencies of the harmonics quoted above.
We can rearrange this to give the string tension: F = 4f12LM.
The most obvious approximation is related to temperament: if the guitar strings were ideal and the frets ideally spaced for equal temperament, tuning harmonic fourths to the E-A and A-D pairs, plus two equal tempered semitones on the D string, would make the interval between lowest E and 2nd fret on the D string about 4 cents flat ((4/3)222/12=1.996). This would lead to interference beats at rates of order one every several seconds. In the context of tuning on a fretted instrument, this is very close.
Another obvious complication with harmonic tuning is that the strings do not bend with complete ease over the nut and bridge (as discussed above). See also How harmonic are harmonics.) As a result, the 1st overtone (the 2nd 'harmonic') on a string is slightly sharper than an octave, the next even sharper than a twelfth, and so on. So tuning the 4th 'harmonic' of the E string to the 3rd of the A string makes them their open interval more than a harmonic fourth. So this tends to compensate for the temperament problem.
A further problem has to do with fret and bridge placement. When you press a string down at the twelfth fret, you increase its length. (Before you press it, the shortest distance between nut and bridge. Afterwards it is longer.) To lengthen it, you have increased its tension. Because of this, and also because of the bending effect at the end of the string, if the 12th fret were midway between nut and bridge, the interval would be greater than an octave. (You can check this experimentally on a fretless instrument.) Consequently, the distance from bridge to the 12th fret is greater than that from the nut to the 12th fret. The effect differs among strings. Some electric guitars have one bridge per string, and individual positioning of each bridge is possible. In other guitars, the bridge is placed at an angle. In a classical guitar, the straight simple bridge necessitates some compromise in tuning. Players can adjust the pitch of a note stopped on a fret by stretching or loosening the string with the stopping finger.
The effects above are difficult measure with experimentally with the required precision: the effects are only a few cents, which is not much larger than the precision of ears or tuning meters when applied to a plucked string. Further, it is difficult to adjust machine heads to achieve a precision better than a couple of cents. On the other hand, if you get all notes in tune within a couple of cents, you are doing better than most musicians and it will sound pretty good!
There are further problems when strings get old. Where you finger them with the left hand, they pick up grease and become more massive (although they may also lose material where they rub on frets). They may also wear where you pick them. As the strings become inhomogeneous, the tuning gets successively worse. Washing them can help.
The way to get around most of these problems is to play fretless instruments, but this makes chords more awkward.
See also How harmonic are harmonics?
|
|
|
|