Entropy, order and dimension
Definitions of entropy
At the molecular level, entropy is related to disorder. But the original definition of entropy is macroscopic; it is the heat transferred in a reversible process divided by the temperature at which the transfer occurs. This definition comes from thermodynamics, a classical, macroscopic theory, part of whose great power comes from the fact that it is developed without specifying the molecular nature of heat and temperature. Originally, entropy had no specific relation to order and it had units of energy over temperature, such as J.K−1.
The Second Law of Thermodynamics says that entropy cannot decrease in a closed system, which is also correctly expressed by comic songsters Flanders and Swann as 'heat cannot of itself pass from one body to a hotter body'. Entropy can decrease, and does so in a refrigerator when you turn it on, but that is not a closed system: the fridge motor compresses the refrigerant gas, raising its temperature enough to allow heat to flow out, a process which exports more entropy into the kitchen than that lost by the cooling interior; the heat is not 'of itself' passing from cold (inside) to hotter: it is pumped out using electrical power provided to the refrigerator. The increase of entropy in a closed system gives time a direction: S2 > S1 ⇔ t2 > t1; increasing time is the direction in which entropy increases in a closed system.
 A molecular interpretation comes from statistical mechanics, the meta-theory to thermodynamics. Statistical mechanics applies Newton's laws and quantum mechanics to molecular interactions. Boltzmann's microscopic definition of entropy is S = kBln W, where kB is Boltzmann's constant and W is the number of different possible configurations of a system. On first encounter, it seems surprising – and wonderful – that the two definitions are equivalent, given the very different ideas and language involved. S = kBln W implies that entropy quantifies disorder at the molecular level. Famously, this equation takes pride of place on his tombstone.
Boltzmann's ideas were inadequately recognised in his lifetime, and he took his own life. Now his tombstone has the final say and he is immortalised in kB and the Boltzmann equation.
A molecular interpretation comes from statistical mechanics, the meta-theory to thermodynamics. Statistical mechanics applies Newton's laws and quantum mechanics to molecular interactions. Boltzmann's microscopic definition of entropy is S = kBln W, where kB is Boltzmann's constant and W is the number of different possible configurations of a system. On first encounter, it seems surprising – and wonderful – that the two definitions are equivalent, given the very different ideas and language involved. S = kBln W implies that entropy quantifies disorder at the molecular level. Famously, this equation takes pride of place on his tombstone.
Boltzmann's ideas were inadequately recognised in his lifetime, and he took his own life. Now his tombstone has the final say and he is immortalised in kB and the Boltzmann equation.
What does Boltzmann's constant mean?
We often write that Boltzmann's constant is kB = 1.38 × 10−23 JK−1. But this is not a statement about the universe in the same way that e.g. giving a value of G does tell us about gravity. Rather, kB = 1.38 × 10−23 JK−1 is our way of saying that the conversion factor between our units of joules and kelvins is 1.38 × 10−23 JK−1. We could logically have a system of units in which kB = 1. (Or we could set the gas constant R = 1: less elegant but it would give a more convenient scale for measuring temperature.) More on that below.
Macroscopic disorder has negligible entropy
In practice, entropy is often related to molecular disorder. For example, when a solid melts, it goes from an ordered state (each molecule in a particular place) to a state in which the molecules move, so the number of possible permutations of molecular positions increases enormously. The entropy produced by equilibrium melting is just the heat required to melt a solid divided by the melting temperature. For one gram of ice at 273 K (0° C), this gives an entropy of melting of 1.2 JK−1.
An important point: this is disorder at the molecular level. Macroscopic disorder makes negligible contributions to entropy. I can't blame the second law for the disorder in my office. To show you what I mean, let's be quantitative. If you shuffle an initially ordered pack of cards, you go from just one sequence, to any of possibly 52*51*50*...3*2*1 = 52! = 8 × 1067 possible sequences. This is a large number, but remember we take its natural log and multiply by kB. So the entropy associated with the disordered sequences is about 3 × 10−21 JK−1. The entropy produced by the heat in your muscles during the shuffling process would be very roughly 1020 times larger. (Just to remind ourselves that 1020 is a large number: the age of the universe is about 4 × 1017 seconds.) So if we are considering the order of macroscopic objects, doing a few example calculations will persuade you that the entropy associated with the number of disordered states times the temperature is negligible in comparison with the work required to perform the disordering or ordering.
The example I often use to stress to students the irrelevance of macroscopic order to entropy is to consider the
cellular order of a human. If we took the roughly 1014 human cells in a human* and imagined ‘shuffling’ them, we would lose not only a person, but a great deal of macroscopic order. However, the shuffling would produce an entropy of only k ln(1014!) ~ 4 × 10−8 JK−1, which is 30 million times smaller than that produced by melting a 1 g ice cube. Again, the heat of the ‘shuffling’ process would contribute a vastly larger entropy.
* The 1014 cells in a human is in itself a nice example of an order-of-magnitude estimate. Cells are about ten microns across, so have volume of about 10-15 cubic metres. A human has a mass of roughly 100 kg so a volume (roughly like the same mass of water) of a tenth of a cubic metre. So 1014 cells in a human — to an order of magnitude. (Wolfgang Pauli was famous for order-of-magnitude estimates, so I like to say that Pauli had one ear, one eye and ten limbs — correct to an order of magnitude). And if you're more interested in entropy and life, here is a chapter I wrote for the Encyclopedia of Life Sciences.
Do life or evolution violate the second law of thermodynamics?
In short, no. It's the second law, not the second whimsical speculation. But how is the negative entropy of producing living biochemistry compensated by entropy production elsewhere? It's worthy of thinking about: life on Earth has a huge number of organisms with wonderful and diverse (cellular and) supracellular order. But the calculation above should tell us that the supracellular order is negligible in comparison with molecular order. Large biomolecules, including DNA and proteins, have a molecular order which, if lost, would produce much more entropy than would losing supracellular order. And there are a lot of organisms, all of whose biochemicals have a combined entropy that is lower than that of the chemicals (mainly CO2 and water) from which they have been made. It's reasonable to ask: Where is that negative entropy compensated? The short answer is that entropy is created at an enormous rate by the flux of energy from the sun, through the biosphere and out into the sky.
Apart from exceptional ecosystems on the ocean floor that obtain their energy from geochemistry rather than from sunlight, all life on Earth depends on photosynthesis, and thus on the energy and entropy flux from the sun and out to space. Plants are (mainly) made from CO2, water and photons. Animals get our energy mainly from plants (or, for carnivores, from animals who ate plants). For the photosynthesis at the base of the biosphere, the input photons come from a star at high temperature, and so have low entropy. The waste heat is radiated at the temperature of the upper atmosphere, effectively about 255 K and out into inter-stellar space.
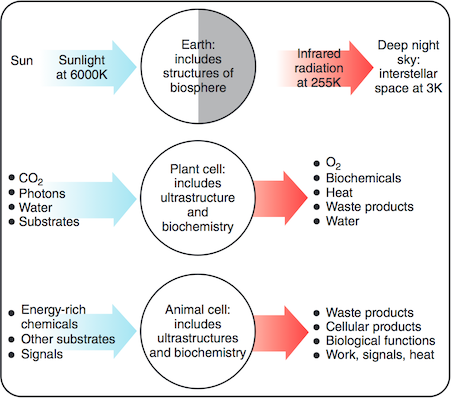
The paper I cited above has this figure showing thermal physics cartoons of the Earth, a photo-synthetic plant cell and an animal cell. Their macroscopically ordered structure – and anything else they do or produce – is ultimately maintained or ‘paid for’ by a flux of energy in from the sun (at ~6000 K) and out to the night sky (which is at ~3 K). The equal width of the arrows represents the near equality of average energy flux in and out. (Nearly equal: global warming is due to only a small proportional difference between energy in and out. Also note the physics convention: blue (high energy photons) is hot and red is cold. The reverse convention probably comes from skin colour.)
In contrast with energy flux, the entropy flux is very far from equal because of the very different temperatures of the radiation in (~6000 K) and out (~255 K): because this temperature goes in the denominator, the rate of entropy export is more than 20 times greater than the entropy intake.
The Earth absorbs solar energy at a rate of about 5 × 1016 W, so the rate of entropy input is about 5 × 1016 W/6000 K ≈ 8 × 1012 W.K−1. The Earth radiates heat at nearly the same rate, so its rate of entropy output is 5 × 1016 W/255 K ≈ 2 × 1014 W.K−1. Thus the surface layers of the Earth create entropy at a rate of roughly 2 × 1014 W.K−1.
Living things contribute only a small fraction of this entropy, of course: this calculation is just to show that there is a huge entropy flux available. Despite the claims of some anti-evolutionists, biological processes are in no danger of violating the Second Law of thermodynamics. Their relatively low entropy biochemicals (and their macroscopically ordered structure, plus anything else they do or produce) is ultimately maintained or ‘paid for’ by a fraction of the huge flux of energy coming in from the sun (at ~6000 K) into plants, through complicated pathways and out to the night sky (at ~3 K). The equal size of the arrows represents the near equality of average energy flux in and out. The entropy flux is not equal: the rate of entropy export is in all cases much greater than the entropy intake. And life on Earth depends on photosynthesis, and thus on this energy and entropy flux. (As for those ocean floor ecosystems, some of their geothermal and geochemical energy might ultimately be traced to the stellar synthesis of the elements, including the radioactive ones that have kept the Earth's core warmer longer than gravitational losses in the Earth's formation would allow.)
And what are its fundamental units? For example, the dimensions of velocity are length over time (and its units are e.g. m/s). In a fundamental sense, entropy doesn't have dimension. Consider the original definition as heat transferred in a reversible process divided by the temperature. Here, heat (measured in joules) is energy. Temperature (measured in kelvins) is proportional to average molecular kinetic energy. So temperature can be measured in joules, too, though it would be an inconvenient size: 'It's 4.2 zeptojoules today (4.2 × 10−21 J), let's go for a swim.' Theoreticians and cosmologists often refer to temperatures in eV. So, in a completely rational set of units, entropy is just a pure number and has no units. So too are Boltzmann's constant kB and the gas constant R. Measuring them in joules per kelvin is a historical accident and Boltzmann's constant is a conversion factor between units, and not a fundamental constant of the universe.
Joe Wolfe,
School of Physics, UNSW Sydney. Bidjigal land. Australia. J.Wolfe@unsw.edu.au
 A molecular interpretation comes from statistical mechanics, the meta-theory to thermodynamics. Statistical mechanics applies Newton's laws and quantum mechanics to molecular interactions. Boltzmann's microscopic definition of entropy is S = kBln W, where kB is Boltzmann's constant and W is the number of different possible configurations of a system. On first encounter, it seems surprising – and wonderful – that the two definitions are equivalent, given the very different ideas and language involved. S = kBln W implies that entropy quantifies disorder at the molecular level. Famously, this equation takes pride of place on his tombstone.
Boltzmann's ideas were inadequately recognised in his lifetime, and he took his own life. Now his tombstone has the final say and he is immortalised in kB and the Boltzmann equation.
A molecular interpretation comes from statistical mechanics, the meta-theory to thermodynamics. Statistical mechanics applies Newton's laws and quantum mechanics to molecular interactions. Boltzmann's microscopic definition of entropy is S = kBln W, where kB is Boltzmann's constant and W is the number of different possible configurations of a system. On first encounter, it seems surprising – and wonderful – that the two definitions are equivalent, given the very different ideas and language involved. S = kBln W implies that entropy quantifies disorder at the molecular level. Famously, this equation takes pride of place on his tombstone.
Boltzmann's ideas were inadequately recognised in his lifetime, and he took his own life. Now his tombstone has the final say and he is immortalised in kB and the Boltzmann equation. 