 |
Answer. The photograph shows the field setting. A cricket team has 11 players so, after counting the number of fieldsmen in view, we conclude that it is unlikely that the bowler will allow the amplitude of the wave function of the ball to be large on the leg side. Diffraction with the bat-pad gap therefore appears highly probable.
 Photo by Howard Burditt, Reuters. Sun-Herald, 24/10/1999.
Photo by Howard Burditt, Reuters. Sun-Herald, 24/10/1999.
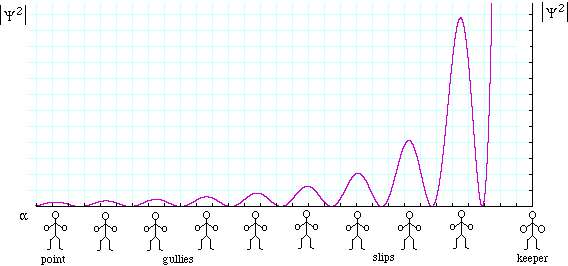
The next diagram, not to scale, shows how the fieldsmen are distributed as a function of θ, the angle through which the ball diffracts after its interaction with the slit between the bat and the pad.
The probability of interaction of the diffracted ball and an observer, including a fieldsman, is proportional to |Ψ2|, where Ψ is the quantum mechanical wave function of the cricket ball. See Single slit diffraction for an explanation, and for a derivation the dependence of |Ψ2| on α, which is plotted below.

The small angle approximation is a bit crude for the angular spacing Δθ, but will suffice for this approximate analysis, so
where Δα is the spacing between maxima of |Ψ2|. Inspection of the graph above shows that, except for the wicket keeper, this spacing is approximately the same as the spacing of the subsidiary minima in |Ψ2|, which requires a phase difference of π. So
where λ is the wavelength of the cricket ball. This is given by the de Broglie equation λ = h/p, where h is Planck's constant. With the exception of some anecdotal claims concerning Jeff Thomson, who retired before the introduction of regular bowling speed measurements, the speed is non-relativistic, so p = mv is a good approximation. Substitution gives
Δθ ~ h/amv, so:
v ~ h/amΔθ = hL/amΔy
Substitution gives a speed of 3 x 10-30 ms-1. This is rather slow: indeed it is less than one atomic dimension per age of the universe. So, to answer question (1): We strongly suspect that no-one can bowl this slowly at ordinary temperatures, but if one is looking for improbable feats from a slow bowler, it is likely to be Shane Warne.
We return now to question (2) about the fate of the batsman. Is he
a) out caught
b) out lbw
c) out interfering with ball?
In fact, given that the sun will have gone out (not down, but out) in the 2 x 1024 years that the ball takes to reach him, we expect that an appeal against the light will be successful.
For cricket lovers: the bowler was Damien Flemming. The batsman was David Mutandera of Zimbabwe. This is
believed to be the first time in cricket history such a field has been
employed in an international one day match. Harare Sports
Club, 23 October 1999.
For an astonishing but real demonstration of diffraction and interference at the quantum level, see Interference of single photons.
Just in case:
Newtonian mechanics (including the fluid mechanics of the air) is completely adequate to describe the behaviour of cricket balls, although the existence, stability and chemical properties of the atoms and molecules of which they are made are all determined by quantum mechanics. So yes, the whole page above is a joke, whose original purpose was not just to amuse first year physics students but more importantly to demonstrate the quite negligible size of quantum mechanical effects in the familiar, macroscopic world. The Brownian motion of the cricket ball (its irregular, random motion due to its collisions with molecules of air) is typically ten billion times greater than the velocity calculated above. The disturbance of quantum mechanical effects such as particle interference by random thermal motion is why even nano-scale quantum effects are often studied at very low temperatures.
A classical question: When does the cricket ball travel its fastest (towards the batsman)?
This question was asked by Dan Trouw of Darwin. Let's answer it using classical mechanics, rather than quantum mechanics, while recognising that quantum mechanics reduces to the classical result in typical macroscopic circumstances, such as cricket.
The question is an interesting one: the ball is released above ground level, so it has a couple of metres to fall. On the other hand, air resistance is slowing it from the moment it leaves the hand. Which force 'wins'? The answer is not immediately obvious – to me, at least. On the one hand, the trajectory of a well-hit ball is obviously not a parabola: it falls more rapidly than one would expect. So the force of air resistance is obviously considerable. On the other, a ball dropped from rest would take a long time to approach terminal velocity. So a calculation is necessary.
The force of gravity is easy, it's the weight, W = mg. Let's compare it with the force Fdrag due to turbulent drag. This is given by:
where v is the speed, ρ is the density of air, A is the cross-sectional area, and CD is the drag coefficient. This coefficient, which is around unity for very blunt objects and which decreases for streamlined objects, must be measured experimentally, For a sphere it is typically about 0.5. So we have
The density of air is about 1.2 kg.m-3. So, for a very fast bowler, with v = 40 m/s, this force is about 2 newtons: for such a bowler, the drag force is about the same as the weight of the cricket ball. For someone bowling at say 20 m/s, the drag force would be only a few tenths of the weight.
Thus, for a ball bowled vertically downwards (a new meaning for shooting one's self in the foot), and for a slow bowler, weight would be more important than drag, as it clearly is when the ball is dropped.
However, the ball is not bowled vertically down -- at least not deliberately. It is easiest to include the effect of direction by considering kinetic energy. The work done by a force is the magnitude of the force times the component of displacement in the direction of the force. Gravity has only about two metres of downwards vertical travel over which to accelerate the ball, while the drag has about twelve metres (more for a slow bowler) to decelerate it. And a very slow bowler would have to bowl the ball slightly upwards ("give it a bit of air") just so that it covers the distance. In which case, gravity would act to slow it at first, not accelerate it.
Consequently, drag has a greater effect on reducing the kinetic energy (and thus slowing it) than has gravity in increasing it. So, even for quite slow bowlers, the fastest that the ball is travelling is just when it leaves the bowler's hand -- until, of course, it reaches the bat.
Links to (more serious) sites about cricket and physics.
- cricinfo.com links to the national sites of many cricket playing countries.
- A cricket page including some notes on the physics of bowling.
- Will it bounce? A discussion of the physics of the effect of the wicket from "Science in Africa".
- Physclips is a (mainly) serious multimedia introduction to mechanics.
- The uncertainty principle: an introduction with some interactive experiments.
- Further educational pages, mainly in physics.
|
Happy birthday, theory of relativity!
As of June 2005, relativity is 100 years old. Our contribution is Einstein Light: relativity in 10 minutes... or 10 hours. It explains the key ideas in a short multimedia presentation, which is supported by links to broader and deeper explanations.