The Soundpost in the Violin: an update

The soundpost introduces an asymmetry to the vibration modes of the body of the violin. It also provides a measure of support similar to the bassbar, for the top plate at a position that is subject to the downbearing of the strings through the bridge feet. It was thought that a “support” post was first fitted in a central position and a connection made with the “pin hole” found in the back of some instruments but this does not seem to be valid. It appears that the pin hole was a compass point for scribing thickness lines for thinning the plate. It is thought that these “support” posts were square in section. It is not known when the soundpost was moved to its present position behind the treble foot of the bridge but musicians were very innovative at the time as indicated by the varying positions of the bridge. It is possible the bridge and the soundpost were moved down at the same time with beneficial results. It would have been easier to install than a central position for the post. Contact with the back was known in some earlier instruments, when the treble foot of the bridge was lengthened and passed through the soundhole leaving the bass foot in contact with the top. It would allow the bridge greater freedom to have a separate “soundpost”.

The properties and mechanics of the soundpost are well known; the history and function as understood up to the year 2000, have been reviewed in an earlier paper [1]. The features of the soundpost to be discussed here are: the stiffness of the post, the main air resonance, the effect on the body mode shape, the stiffness as seen at the bridge foot positions, and the sound level as a function of the soundpost position.

The stiffness of the Soundpost

Soundpost material is split along the grain so the elastic modulus is a maximum and this leads to maximum stiffness along the length of the post. This stiffness is determined by the dimensions being proportional to the diameter and inversely proportional to the length:

            Stiffness, s = Ea/l

where E is the elastic modulus along the grain, “a” is the cross sectional area and “l” is the length of the soundpost. Another relation is the mechanical impedance, Z = √(sm) where “s” is the stiffness and “m” is the mass of the soundpost. Both relations have been used in earlier papers.

It was found [2] that a stiffness larger than 6 MN/m was desirable for a soundpost. Soundposts in use easily meet this requirement. The equivalent impedance minimum was about 60 kg/s. In the past, modifications to the shape of the soundpost by hollowing or thinning the middle of the length have served to lower the stiffness.

The main air resonance

The main air (or Helmholtz) resonance does not require the presence of the soundpost.  An example from [3] table 9.7 on page 184, shows A0 at 250 Hz and effective stiffness 98 N/m with no soundpost. With a soundpost at the standard position, 5/22, A0 was 283 Hz and the effective stiffness 125 N/m. With the body made immobile A0 became 292 Hz and the effective stiffness 133 N/m. The body stiffness (compliance) changed from 370 N/m (3 mm/N) with no soundpost to 2 kN/m (0.5 mm/N) with a soundpost. As pointed in [3] the compliance of the body may be a useful measure of its ability to radiate sound.

A0 is a very good radiator. The soundpost introduces a small island in the top that is in phase with the back. The area of this island should be as small as possible to maintain the maximum area of the top acting in phase. This resonance uses the “spring” of the air in the violin working with the vibrating “mass” of air in the soundholes to resonate at about 280 Hz. With no soundpost, the compliance of the body adds about 700 cc to the volume and with a soundpost the effective volume increases by 130 cc. The strength of the main air resonance, A0, is governed by the vibrating mass in the soundholes and this is determined by the volume in the violin and the frequency required.

The effective mass (and stiffness) for the main air resonance with and without a soundpost are given in [3]. It is shown that a soundpost raises the effective mass and the stiffness of the body considerably; an almost identical result was obtained for a similar violin (No 2) as shown in table 9.6 on page 183 of the same reference. The first result was found by adding small weights near the bass foot of the bridge, an antinodal region, to obtain df/dm while in the other, df/dm was found by changing the temperature of the atmosphere. In both cases, as well as the one with no soundpost, A0 had a low radiation resistance and was therefore a good radiator. The parameters discussed above are explained in Chapter 5 of [3] page 68. The calculated mass of the air plug in the f-holes of 40 mg (chapter 9 of [3]) compares well with that determined experimentally of 34 mg (tables 9.1 and 9.6). Without the soundpost, the effective mass and stiffness were about one third of that with the soundpost. The violin is more compliant but no explanation is offered for the low effective mass.

Body modes The soundpost has an influence on the positions of the nodal lines that delineate the vibration modes of the body resonances. Only the resonances below 1 kHz are spaced apart sufficiently for their nodal lines to be studied. The main body resonances, B1- and B1+ are discussed here. The appearance of the nodal lines for these two modes, with and without a soundpost, is shown in figure 1. 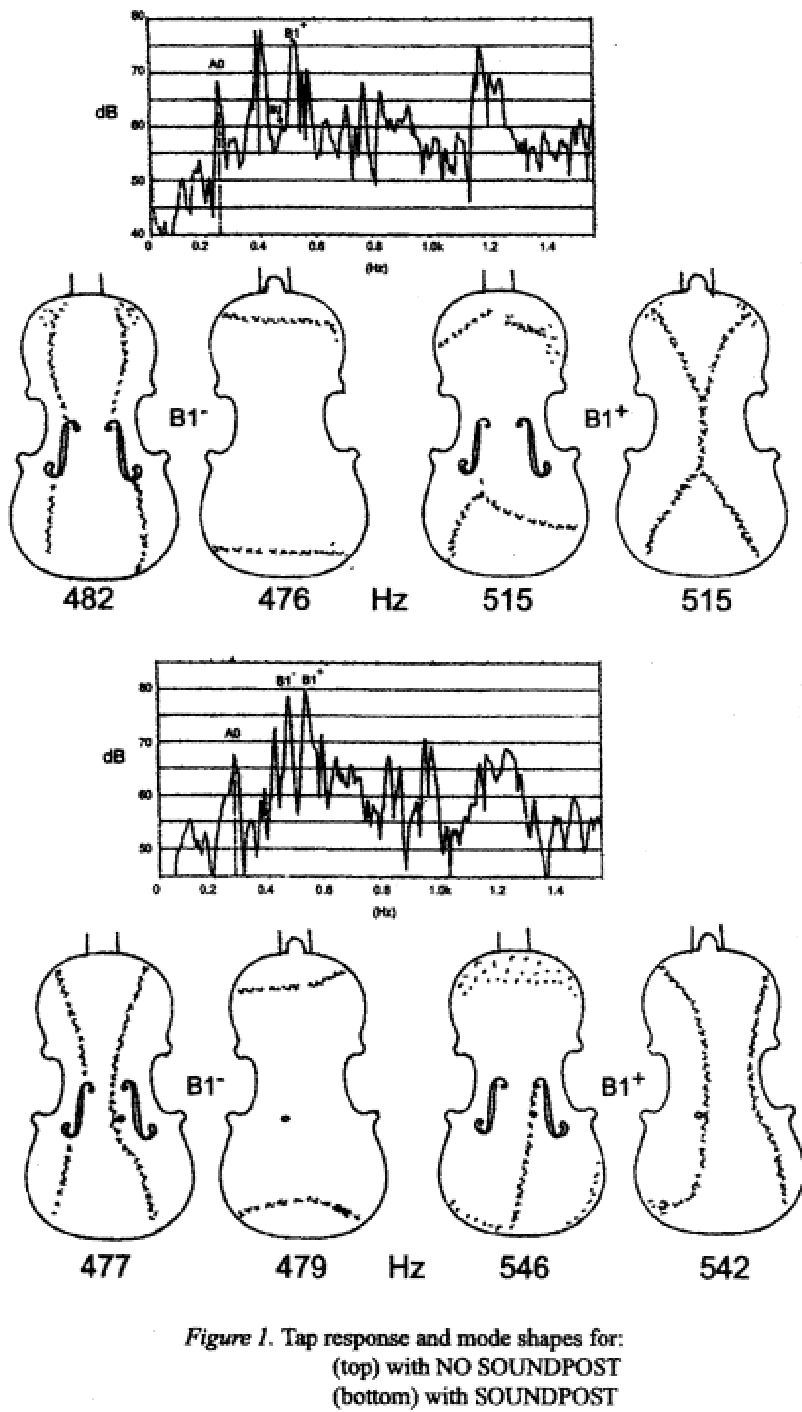This example, taken from [2] for violin No 1, may not be representative for all violins because of differences in arching and thicknessing between their tops. Different positions of the soundpost may also have an effect. In this figure the soundpost was behind the treble foot of the bridge. For B1- the nodal line in the top has been moved away from the f-hole. The absence of a resonance peak in the tap response at B1- with no soundpost is hard to explain. It might be the case if the bridge is rocking symmetrically. For B1+ the soundpost pulls the lower nodal line in the top to its position near the bridge, while in the back, the nodal lines are converted to appear similar to those for B1- in the top. These nodal patterns are of interest because of their effect on the monopole radiation, which is important for a strong fundamental [4]. The nodal pattern has to be optimised to produce a strong monopole component. Stiffness at the bridge feet positions The horizontal vibration of the strings is partly resolved into a vertical force that excites the body of the violin to produce the sounds we hear. For maximum output the violin needs to have a mechanical impedance that is not too high, but it should not be too low that wolf notes are produced. Measurement of stiffness at the bridge is of interest in this context. It can be measured either at the bridge top or at the bridge feet. The latter would be a measure of the resistance of the body. The earlier measurements [5] for violin No 1, were made at the G and E string slots and therefore were influenced by both the body and the bridge. Table 4 in that paper showed that without a soundpost the stiffness at both string slots was low; 33 kN/m at the G string slot and 42 kN/m at the E string slot. With a soundpost at the standard position i.e. 5 mm behind the treble foot of the bridge, the stiffness at the G string slot was raised to 41 kN/m and at the E string slot to 67 kN/m. At 5 mm inside the treble foot the stiffness at the G string slot was 36 kN/m and at the E string slot 60 kN/m. At 5 mm outside the treble foot, the stiffness at the G string slot was 40 kN/m and at the E string slot 77 kN/m. There was a rise in stiffness at the E string slot moving from inside the treble foot to outside the treble foot with the stiffness at the G string slot staying roughly the same. The stiffness found at the G string slot remains unchanged for other positions of the soundpost i.e. under the treble foot and 10 mm behind it. To determine the stiffness of the body alone, direct loading without the bridge, at the treble and bass foot positions gave consistent results although with a different violin, No 2. This is illustrated in figure 2.

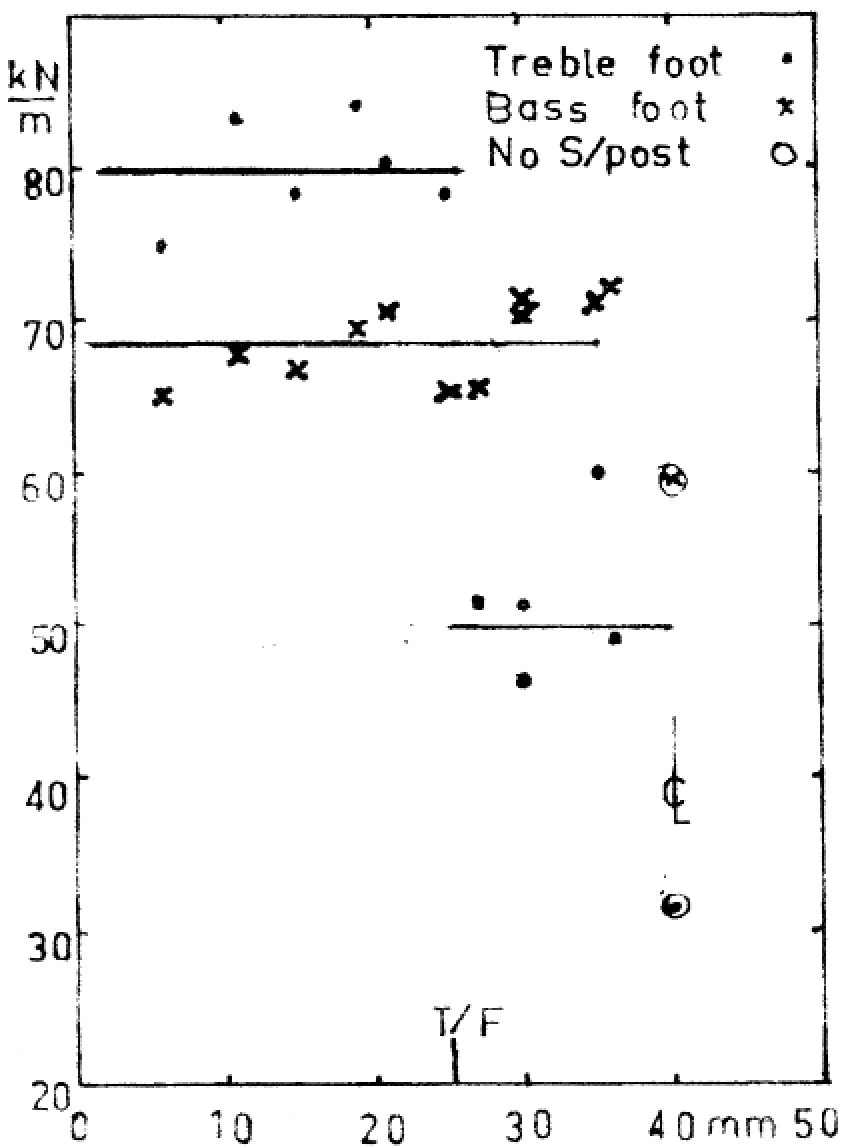
Figure 2 at right: Stiffness at bridge foot positions as a function of the distance of the soundpost from the inner edge of the treble f-hole. These extended results appear elsewhere [6]. Figure 2 shows that, within experimental error, the stiffness of the violin at the bass foot position is about 70 kN/m for all positions of  the soundpost. At the treble foot position, with the soundpost between the f-hole and the bridge foot position, the stiffness is higher, at about 80 kN/m. With the soundpost inside the treble foot, the stiffness drops to about 50 kN/m. The interesting thing about this is when the soundpost is behind the treble foot of the bridge (T/F in the figure) the stiffness could have either of two extreme values depending on the exact position. This result may explain the sensitivity of the sound to the soundpost location in this area? The “safe” position for the soundpost will therefore be outside the treble foot, and as a secondary consideration in a position to minimise the area of the “island”. The effect on sound level The Saunders Loudness Test provides a practical way to assess the sound level as a result of experimental changes such as soundpost position. The sound level meter is best placed about a metre from the violin in the plane of the instrument on the treble side. Consistent firm bowing is required to produce a loud “musical” output. The sound level recorded at each semitone for an octave on each string is plotted against the note position for, in this case, each position of the soundpost. Figure 3 from [5] shows the effect of three soundpost positions as well as one for the absence of the soundpost.

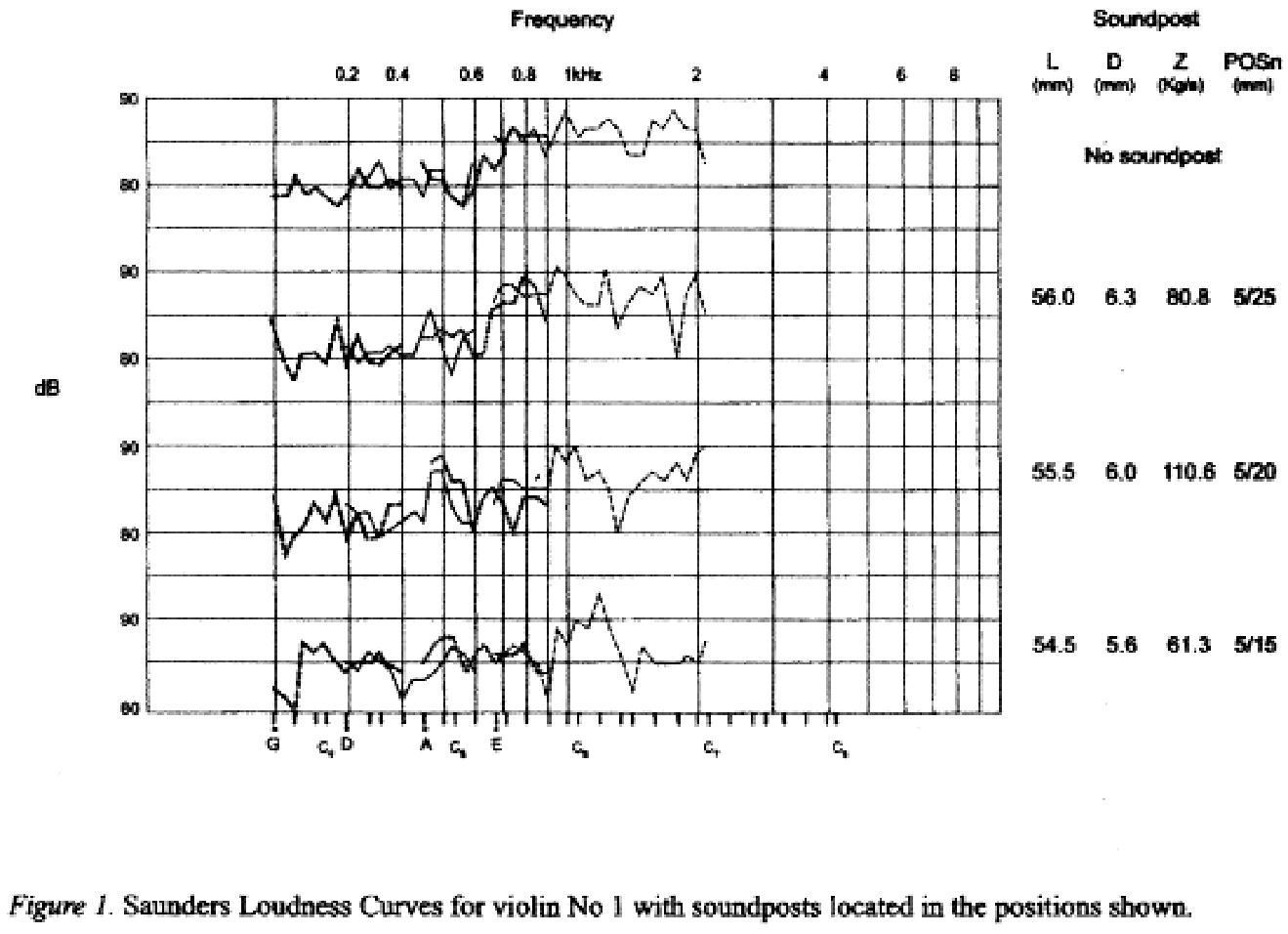
Figure 3 Saunders Loudness Plots for violin No1 with three soundpost positions. Without a soundpost the lower strings, in this figure, have a sound level around 80 dB; the top string produces a level on average about 6 dB higher. There is a rough division in that the fundamentals of the lower strings rely on the monopole component or breathing action of the body below about 1kHz. The harmonics most of which are above 1kHz are supported by plate modes and are more directional whereas the fundamentals radiate more or less equally in all directions. As the soundpost is moved from between the bridge feet to outside the treble foot, the sound level of the lower strings is raised towards that of the top string. Directly behind the treble foot is an area of uncertainty as suggested by figure 3. The sound associated with three conditions; no soundpost, a soundpost inside the treble foot and one outside the treble foot for violin No 2 can be heard in [6]. Discussion The continuing interest with the soundpost lies in its influence on balancing the sound output from the violin. The sound quality has already been set by the distribution of resonances in the response. The current attention to gradual improvement in output by small changes in the formation of the instrument would seem to have reached a limit. A major change would appear to be required. Such a change was indicated by the scaling of the size of the violin from the currently accepted body length of 14 inches to one of 15 inches by C. M. Hutchins and J. C. Schelleng [7]. The gain in output was about 5 dB. These authors maintained the same string length and diapason as that of the 14 inch violin. Players commented that this may also have been scaled for the larger size instrument with advantage. The sides were reduced to about 22 mm and the f-holes adjusted to maintain the same A0 frequency. It would appear that there is some scope for variation in the sides and f-holes as well as the setup for this enlarged violin. The body resonances have to remain in the same place as for the instrument as we know it. The effect of the soundpost position on the nodal patterns of the other resonances e.g. C2 and resonances higher than B1+ that can be isolated for study, may be of interest in maximising the monopole content of the radiation [8]. The importance of the stiffness at the bridge feet positions in relation to the location of the soundpost has to be further tested. The stiffness of the bassbar is also an important variable that has not been investigated. It would appear that the soundpost can be placed between the treble foot of the bridge and the f-hole with safety. It has not been possible to find a link between the plate tuning frequencies and the frequency of the main body modes. The current understanding seems to be to preserve the octave relationship between the three prominent lower modes of the free top plate and between the two upper modes of the back even though the frequency of mode #1 in the back is high and to match mode #2 in the two plates. It was also desirable to keep the frequencies as high as possible while having a low plate mass. Mode #1 in the top plate was not to be lower than 92 Hz. Plate frequencies (mode #5) for classical violin tops have mostly been in the low 300 Hz range while body modes have ranges from the mid 400 Hz to the low 500 Hz with no apparent connection. Sacrificing the octave relationship in the top by installing a lighter bassbar leading to a lower top plate stiffness at the bass bridge foot may give a higher output, other parameters being kept the same. The measurements of stiffness quoted here were made by static loading. They may be of value at low frequencies. The effect of resonances, particularly those of the bridge and body, are expected to influence the dynamic stiffness with as yet unknown results. The influence of the bassbar may gain increased importance in understanding the stiffnesses in the central area of the top plate.

References

The references listed can be accessed at this website except for [7].

1. McLennan J. E. “The soundpost in the violin” Jnl AAMIM vol XIX (3) 2000, 17-37.
2. McLennan J. E. “The soundpost in the violin. Part I: The effect of soundpost stiffness on peak resonance and sound output” J. AAMIM vol XX (1) 2001, 24-35.
3. McLennan J. E. Doctoral Thesis “The violin: music acoustics from baroque to romantic” Table 9.1 p 174. www.phys.unsw.edu.au/music/people/mclennan.html
4. McLennan J. E. “Monopole radiation at low frequencies in the violin” www.phys.unsw.edu.au/music/people/mclennan.html
5. McLennan J. E. “The soundpost in the violin Part II: The effect of soundpost position on peak resonance and sound output” J. AAMIM vol XX (2) 2001, 16-27.
6. McLennan J. E. “The effect of the soundpost on violin sound’’ www.phys.unsw.edu.au/music/people/mclennan.html
7. Hutchins C. M. and Schelleng J. C. “A new concert violin” J. Audio Eng. Soc. Vol 15 (4) October 1967.
8. McLennan J. E. “Monopole radiation at low frequencies in the violin” www.phys.unsw.edu.au/music/people/mclennan.html

John E McLennan

MSc, Phd, UNSW, ASTC (Dip Met), AIM (Lond), C Eng