Chladni patterns for guitar plates
Chladni patterns show the geometry of the different types of vibration of the guitar top plate. This site has an introductory explanation of modes of vibration and a library of photographs of the Chladni patterns of a guitar top plate and an intact guitar.
The results reported on this site are part of a practicum project by Thomas Erndl a visiting student from Fachhochschule Regensburg, Germany.
Modes of vibration
(See also the explanations of the guitar, and Strings, harmonics and standing waves.) A mode of vibration is just a way of vibration. Think what happens when you strike a xylophone bar in the middle and set it vibrating. The bar is supported at two points towards the ends. The simplest mode of vibration is this: when the middle of the bar goes up (as shown by the solid lines in the figure) the ends of the bar go down. When the middle goes down (dashed lines), the ends go up. The two points that do not move are called nodes and are marked N in the diagram. (If "modes" and "nodes" sound confusing, remember that the node has no motion.)
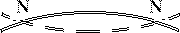 Sketch of a simple mode of vibration. Sketch of a simple mode of vibration.
This first mode of the xylophone bar is rather similar to a mode of vibration of a simple rectangular plate which is called the (0,2) mode (the naming convention is explained below.)
Photographs of the Chladni pattern of:
mode (0,2) of a uniform rectangular aluminium plate.
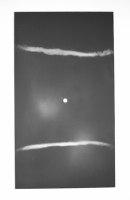 In this pictures, the lines are formed from sand that has collected at the nodes, but has been shaken off the moving regions. The top plate of a guitar is more complicated in shape, and so the nodes also have a more complicated shape. White sand was used for the black-painted aluminium plate, and black sand for the guitar top plate.
In this pictures, the lines are formed from sand that has collected at the nodes, but has been shaken off the moving regions. The top plate of a guitar is more complicated in shape, and so the nodes also have a more complicated shape. White sand was used for the black-painted aluminium plate, and black sand for the guitar top plate.
Why are there nodes?
The supports of the xylophone bar do not cause the nodes, rather they are placed at the positions which are nodes so as to facilitate this vibration. In an object which is not firmly clampled, a vibration cannot easily move the centre of mass of the object. It follows that, if some part is going up, another part is going down. In the simple motion at resonance, the point(s) that divide(s) these regions are nodes. When a violin or an isolated part is vibrating, the centre of mass doesn't move much, so once again it can be divided into parts that are going up and others that are going down. In these simple modes of vibration, the motion of different parts is either exactly in phase or exactly out of phase, and the two regions are separated by nodes. The nodes are points for a quasi one-dimensional object like a string, or lines for a quasi two-dimensional object like a plate. (There is more explanation in Strings, harmonics and standing waves.)
Modes of guitar plates
 
One of the modes is comparable with a mode of vibration of a rectangular plate. In this mode the nodal lines separate the plate in three parts, so it can be compared with the (0,2) mode of the rectangular plate, with the middle part moving 180° out-of-phase with the ends.
The modes for the guitar plate are complicated by the presence of the sound hole and the bracing.
More guitar Chladni patterns.
How are Chladni patterns formed?
There are at least three different methods.
- The plate can be made to resonate by a powerful sound wave which is tuned to the frequency of the desired mode.
- The plate can be bowed with a violin bow. This is easiest if one choses a point that is a node for most of the modes that one doesn't want, but not for the desired node.
- The plate can be excited mechanically or electromechanically at the frequency of the desired mode.
For the photographs on this site, a small (4g) magnet was fixed to the bridge. An oscillating magnetic field (provided by a coil connected to an audio amplifier and a signal generator) was used to provide an oscillating force whose frequency is tuned to the resonance of the mode. Experiments using different masses showed that the mass of the magnets caused us to underestimate the frequency by about 10 Hertz in some cases. But there were also patterns obtained with a magnet which could not be obtained without a magnet (e.g. by a speaker). That means, that the vibrating system has changed qualitatively by adding the magnet to the plate.
In all cases, some finely divided material is placed on the plate. The material used here is fine sand. When the plate resonates, the motion becomes large over most of the surface and this causes the sand to bounce and to move about. Only at or near the node is the sand stationary. Thus the sand is either bounced off the plate or else collects at the nodes, as shown in the photographs.
Why are Chladni patterns useful?
The adjustment of the top plate is important to the properties of the final instrument. The most important adjustments are thinning the wood towards the edge of the plate, and thinning the braces. Chladni patterns provide some feedback to the maker during the process of adjusting the plate to its final shape. Symmetrical plates give symmetrical patterns; asymmetrical ones in general do not.
It is very difficult to relate the frequencies of the modes of the isolated top plate to those of the modes of a finished guitar. Fortunately, adjustments can be made to an intact instrument: thinning the top plate close to the edge, and adjusting the bracing by reaching through the soundhole with specially shaped tools. The "tuning" of plate resonances is less formalised in guitar making than in violin making. Over the centuries, violin makers have discovered empirical relations between the modes of free plates and the properties of the finished instrument. Many scientists have been interested in the acoustics of violins, and many violin makers have been interested in science, so a lot has been written about the acoustical properties of violins and their parts. See:
- "Research Papers in Violin Acoustics", CM Hutchings and V Benade, eds, Ac.Soc.Am. 1996
- "The acoustics of violin plates" by Hutchins, C.M. Scientific American, Oct.1981, 170-176.
- "Experiments with free violin plates" by Jansson, E.V., Moral, J.A. and Niewczyk, J. J. CAS Journal Vol 1 No 4 (Series II) 1988.
- "The Physics of Musical Instruments" by Fletcher, N.H. & Rossing,T.D. Springer-Verlag, New York, 1991.
- Mode Tuning for the Violin Maker by Carleen M. Hutchins and Duane Voskuil CAS Journal Vol. 2, No. 4 (Series II), Nov. 1993, pp. 5 - 9
- The Catgut Acoustical Society home page
More Chladni patterns
Some explanatory notes and related pages on this site
Some links to related sites
|

