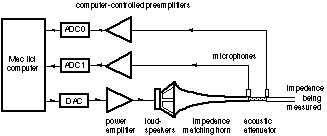
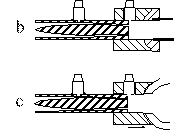
Figure 1. The impedance spectrometer (a) and the configuration for calibration (b) and for measurement (c). The figure is not to scale.
Acoustics of classical and modern flutes - impedance spectra,
sound spectra, sounds and fingerings
Joe Wolfe, John Smith, John Tann and Neville H. Fletcher
The modern flutes studied were production line instruments (Pearl PF-661, closed hole, C foot and B foot). On these mass produced instruments, both the open and closed hole variants use the same 'scale' (i.e. positioning of tone holes). For standard measurements, the position of the cork in the head joint was set at 17.5 mm from the centre of the embouchure hole, and the tuning slide was set at 4 mm. These values are typical values used by flutists playing at standard pitch.
The classical flute was made by Terry McGee of Canberra, Australia. The dimensions of the instrument are based on those of a large-hole Rudall and Rose flute (R & R #655 from the Bate Collection in Oxford) but the scale has been adjusted to play at 440 Hz. It has a head joint, a joint with three tone holes closed by the fingers of the left hand, a further joint with three tone holes closed by the fingers of the right hand and one mechanical key, normally closed, whose opening makes the transition from E4 to F4 or from E5 to F5. It has three interchangeable feet: one is a C foot in the classical style, modelled on the Rudall and Rose instrument. Another is a D foot: it plays D4 with all holes closed. The third foot is also a C foot, but its bore is larger than that of the classical foot, and the bore increases slightly at the end. This foot was designed for use in Irish music, which often uses flutes of the classical design. This flute is made of gidgee wood (Acacia cambagii).
The Baroque flute was made by Terry McGee of Canberra, Australia. It is an unscaled replica of an instrument made by J.A. Crone in Leipzig in about 1760. It plays at A=415. (This paragraph, not in the original manuscript, was added in late 2001 when the baroque measurements were added to the data base.)
Most measurements were made at T = 25±0.5°C and relative humidity 58±2%. Both of these values are considerably lower than those in flutes being played, and thus the features of the measurements here occur at frequencies about two percent lower than they would be on a flute being played (about 30 cents flat). We judged that correcting for a different value of the speed of sound was easier than the inconvenience of operating at high temperature and humidity. Further, the temperature and humidity are presumably functions of position in the flute being played, and these conditions are difficult to reproduce in the spectrometer. (Cork and tuning slide position, temperature and humidity were also varied to determine their effect on relative and absolute tuning, and on harmonicity. These results will be discussed elsewhere.)
The impedance spectrometer is shown in Figure 1a. The signal is synthesized on a computer and output via a 16-bit AD card (National Instruments NBA-2100) to a power amplifier and pair of loudspeakers. An exponential horn (cut-off frequency 200 Hz) matches the speaker to the attenuator.
The attenuator comprises a truncated conical plug located inside, and coaxial with, a truncated conical hole. The two conical surfaces are spaced by three straight pieces of fine wire (diameter 120 mm) placed at 120° intervals in the annular space between them. The input side is shaped as shown (Figure 1b) to improve further the impedance matching. The choice of the output impedance of the attenuator is a compromise between a high value, which improves the accuracy for high measured impedances, and a low value, which allows a greater current, higher signal-to-noise ratios and therefore better precision for low impedance measurements.


Figure 1. The impedance spectrometer (a) and the configuration for
calibration (b) and for measurement (c). The figure is not to scale.
Small electret microphones are mounted at either end of the attenuator. Only the downstream microphone is used for calibration and measurement. The upstream microphone is used in a preliminary experiment to put an upper bound on the effect of reflections from the downstream end the attenuator. The output of the attenuator is a tube of 7.8 mm internal diameter, equal to that of our calibration reference and slightly smaller than the embouchure hole of each flute.
Our reference impedance for calibration is a 'semi-infinite' cylindrical waveguide: a straight, stainless steel pipe of 7.8 mm internal diameter. Its impedance is therefore purely resistive. Its length of 42 m was determined by the width of the Physics building. At 200 Hz, a tube of this diameter has an attenuation coefficient of 0.11 m-1 = -1.0 dB.m-1 [1] so the echo returns with a loss of 80 dB or greater. (The dynamic range of the instrument is a little greater than 80 dB, but the precision is less than this. The echo returning during calibration coincides with a frequency component of the input which is 80 dB or more greater, and so can be ignored.) Its impedance is therefore resistive, with resistance equal to its characteristic impedance, Rref = 8.5 MPa.s.m-3. Swagelok fittings are used to connect the elements. The 'semi-infinite' pipe is enclosed in a plastic pipe for sound insulation, and the plastic pipe is mounted from the ceiling via rubber bushes. The use of a frequency independent reference impedance improves the signal-to-noise ratio over the whole range, and obviates the need for more than one microphone in routine calibration or measurement.
Before calibration, the desired dependence upon frequency of the acoustic current uref(f) is chosen. If noise is distributed approximately equally across frequencies, it is advantageous to use a signal that is frequency independent to achieve uniform signal-to-noise ratio. For these experiments, in which low frequency noise was not a major problem, the acoustic current was therefore chosen to be independent of frequency. A voltage waveform Vref(f), with frequency independent harmonic components over the desired range, was synthesized and input to the power amplifier. The acoustic pressure is measured with the downstream microphone and sent via low noise preamplifiers, whose gain is computer controlled, to the AD card. The pressure spectrum pref(f) is calculated. pref(f) includes the frequency dependence of the AD card, amplifiers, speakers, horn, attenuator, other plumbing and microphone. A calibrated waveform is then synthesised with Fourier components Vcal(f) proportional to Vref/pref(f). This signal is then output, via the same elements, to the reference impedance. The microphone now returns a calibrated spectrum pcal(f), in this case a 'flat spectrum', i.e. a signal whose Fourier components are essentially independent of frequency. These pcal(f) are recorded. The relative phases of the harmonic components of Vref are adjusted to improve significantly the signal to noise ratios of our measurements [2].
Finally, the performance of the spectrometer was checked by measuring the impedance of a series of open, stainless steel cylinders, for which the input impedance was calculated using the radiation impedance as the termination at the open end [1], and values of the speed of sound from [3] (Figure 2). The theoretical curve is not shown because it obscures almost all points. The discrepancies between theory and experiment occur when Z(f) approaches 100 MPa.s.m-3, where the finite output impedance limits the precision, as discussed below.
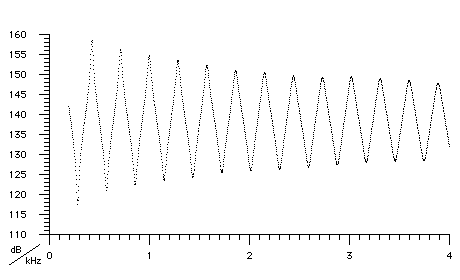
Figure 2. Z(f) for an open, stainless steel cylinder of length 596.7
mm and diameter 7.8 mm.
For measurements of acoustic impedance very much less than that of the attenuator, the spectrometer source may be approximated as an ideal current source and so the acoustic current equals uref(f). The output of the attenuator is effectively in parallel with the system being measured, so the attenuator conductance was subtracted from both calibrations and measurements. From the dimensions of the attenuator we calculate a characteristic impedance for the attenuator Za = 170 MPa.s.m-3. The actual impedance is likely to differ a little, because the spacing wires are not perfectly straight. We therefore determine the value of Za by measuring known loads with high impedances, which in this case were the first maxima in the impedance spectra of open stainless steel cylinders. This gives a value of 155 MPa.s.m-3. The attenuation of the travelling wave in the narrow space between the cones is large, so the attenuator output is expected to behave like a pure resistance-another semi-infinite wave guide. This assumption requires that the wave travelling from the output of the attenuator, back to the input of the attenuator and then back to the output may be neglected. To check this, the upstream microphone was used to measure the pressure waveform at the input of the attenuator during calibrations (where the load was 8.5 MPa.s.m-3, independent of frequency) and measurements on cylinders with strong resonances (where Z(f) varied from 20 kPa.s.m-3 to 200 MPa.s.m-3). No measurable difference was observed, so the attenuation in this wave is sufficient to permit its neglect in the measurements.
Thus the subtraction of the attenuator conductance should allow precise measurements less than about 100 MPa.s.m-3. This exceeds the maxima in Z(f) of the flute where, in any case, the minima are of much greater interest. (For measurements on other wind instrument families, where the maxima are of greater interest than the minima, the same technique may be used with a higher value output impedance.)
The response of the flute to the driving force provided by an oscillating air jet is inversely proportional to an impedance Z(f) that is the sum of the input impedance of the flute tube as measured on a plane at the exterior entry to the embouchure hole plus the radiation impedance of the embouchure hole measured on this same plane [1, 5]. Because it is relatively straightforward to estimate the value of this radiation impedance, our approach involves replacing it by the impedance of an appropriate short length of tube fixed to the exterior of the embouchure hole, and then measuring the input impedance of the flute at the outer end of this tube.
The impedance head used here (Figure 1c) is designed to allow a measurement that, without any further corrections, approximates the input impedance of the flute under typical playing conditions. The dimensions are several mm and the frequencies of interest (< 3 kHz) have wavelengths longer than 100 mm, so the plane wave approximation should be good at low frequencies and acceptable at high frequencies.
As discussed above, the impedance head includes a short length of tube designed to compensate for the effects at the embouchure hole under playing conditions. The radiation impedance of a baffled pipe is approximately equal to that of an ideal tube with a length about 0.85 a, where a is its radius. In the absence of the player's face, the radiation load at the embouchure would therefore be approximately that of a pipe with the same area and length 0.85 a. In practice, the equivalent length is longer because the player's lower lip occludes part of the hole and his face acts as a baffle, reducing the solid angle available for radiation.
Let the player's lips leave open a fraction g of the hole, and assume that the face leaves open a fraction h of the solid angle available for radiation. The radiation impedance would then be
| (1) |
where Semb is the area of the embouchure hole (about 90 mm2). We use a pipe with smaller cross-section than the embouchure hole so that positioning of the impedance head is not critical. The impedance Zc of the coupling section of the pipe that is to simulate the radiation load, is
| (2) |
where Lc is the length and Sc the cross sectional area. We use a value of 6 mm for Lc. This is chosen empirically so that, at the corresponding temperatures and humidities, the impedance minima correspond to the played notes. Therefore
| (3) |
which approximately corresponds to g = h = 0.5.
The effect of changing g and h can therefore be simulated by changing Lc. Further, this can be done theoretically using the transfer matrix for a cylindrical pipe where, for this length, losses may reasonably be neglected [1].
The impedance head, including the microphones and attenuator, were connected to the flute via the adaptor as shown in Figure 1c, which is acoustically equivalent to a cylinder. The adaptor has the same radius as the calibration cylinder and is 6.0 mm long. This load may be removed by calculation from the resultant measurement, but its dimensions were chosen so as to give an impedance equivalent to that of the radiation impedance of the embouchure hole under typical playing conditions (see the previous section and [4] for more details). A thin gasket made of flexible casting compound (Wacker Elastosil M4503, Barnes, Sydney) is used to seal the measurement head to the flute.
The reference signal is applied to the flute and the Fourier components pmeas(f) are then measured. The total admittance pcal(f)/(pmeas(f).Rref) is calculated, and the attenuator conductance is subtracted to give the flute admittance. When measurements are finished, the spectrometer is reconnected to the reference impedance and a measurement is taken to compare with the calibration.
Background noise in the laboratory, although rather quiet, could affect measurement of the weak pressure signals at the impedance minima. For this reason, the musical instrument, or other load to be measured, was placed inside a rigid box, which was lined with acoustically absorbent materials to minimise resonances of the box. The operator (who is also a flutist) passed his arms through rigid 'sleeves' on the box to finger the instrument and triggered measurements with a foot control.
Because sound spectra depend very strongly on parameters determined by the player, by the radiation pattern of the flute, and by recording conditions, sound spectra recorded for human players can only be regarded as examples. The obtaining of examples typical of playing by a flutist under realistic, musically comfortable conditions are not consistent with obtaining exactly repeatable spectra. Sound spectra were measured at a distance of about 1 m directly in front of the player in a room that was moderately quiet and with little reverberation. The player, Geoffrey Collins, is one of Australia's foremost flutists. The notes were written out in traditional musical notation, with dynamic markings ff, mf and p. Where the fingerings were not standard, they were indicated using a fingering diagram of the sort shown in Figure 3. For the classical flute, he used the McGee instrument described above. For some of the notes on the modern flutes, he used the Pearl flutes discussed above. For the rest of the notes and multiphonics on the modern flute he used one of his own flutes, which is a hand-made Brannen-Cooper flute with a Nagahara head.
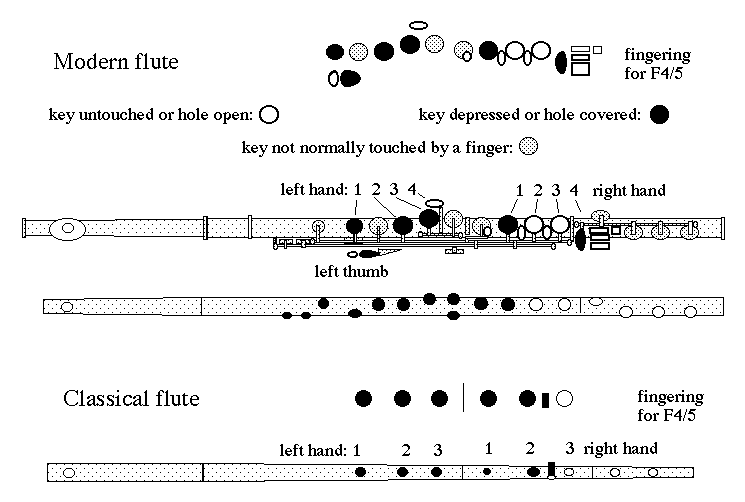
Figure 3. Fingering and acoustic schematic diagram
for the modern and classical flutes. From the top are shown a fingering diagram
for the modern flute, a sketch of the modern flute and an acoustic schematic
of that instrument. Next is a fingering diagram and schematic for the classical
flute. A similar legend is used for all the fingerings and notes in the data
base. The example chosen here is the fingering for the notes F4 and F5.