Helmholtz Resonance

Analysing the Helmholtz resonance
Resonance, impedance, phase and frequency dependence
Complications involving the length
Helmholtz resonances and guitars

Analysing the Helmholtz resonance

Now let's get quantitative: First of all, we'll assume that the wavelength of the sound produced is much longer than the dimensions of the resonator. For most bottles, and for an ocarina, the wavelengths turn out to be tens of cm to a few metres, so this approximation is pretty good, but it is worth checking whenever you start to describe something as a Helmholtz oscillator. The consequence of this approximation is that we can neglect pressure variations inside the volume of the container: the pressure oscillation will have the same phase everywhere inside the container.

Let the air in the neck have an effective length L and cross sectional area S. Its mass is then SL times the density of air ρ. (Some complications about the effective length are discussed at the end of this page.) If this 'plug' of air descends a small distance x into the bottle, it compresses the air in the container so that the air that previously occupied volume V now has volume V − Sx. Consequently, the pressure of that air rises from atmospheric pressure P_A to a higher value P_A + p.

Now you might think that the pressure increase would just be proportional to the volume decrease. That would be the case if the compression happened so slowly that the temperature did not change. In vibrations that give rise to sound, however, the changes are fast and so the temperature rises on compression, giving a larger change in pressure. Technically they are adiabatic, meaning that heat has no time to move, and the resulting equation involves a constant γ, the ratio of specific heats, which is about 1.4 for air. (This is explained in an appendix.) As a result, the pressure change p produced by a small volume change ΔV is just

Now the mass m is moved by the difference in pressure between the top and bottom of the neck, i.e. a nett force pS, so we write Newton's law for the acceleration a:

substituting for F and m gives:

So the restoring force is proportional to the displacement. This is the condition for Simple Harmonic Motion, and it has a frequency which is 1/2π times the square root of the constant of proportionality, so

Now the speed c of sound in air is determined by the density, the pressure and ratio of specific heats (c = (γP/ρ)^½), so we can substitute that in the equation above and write:

Let's put in some numbers: for a 1 litre bottle, with S = 3 square centimetres and L = 5 centimetres, the frequency is 130 Hz, which is about the C below middle C. (See notes.) So the wavelength is 2.6 metres, which is much bigger than the bottle. This justifies, post hoc, the assumption made at the beginning of the derivation.

Resonance, impedance, phase and frequency dependence

This section can be read on its own, but if you want more detailed background, see Oscillations, Forced Oscillations and Acoustic compliance, inertance and impedance.

Let's return to the mechanical representation and look at the Helmholtz resonator from the outside, as shown in the first schematic: we are pushing with an oscillatory force F, with frequency f ,the mass m (the air in the neck of the resonator), which is supported on the spring (the enclosed air) with spring constant k, whose other end is fixed (the air in the resonator can't escape). Unrealistically, we'll neglect gravity and friction (for now).

circuit diagram of Helmholtz resonance

The force required to accelerate the mass is proportional to the acceleration and so proportional to f². At sufficiently low frequency, the force required to accelerate the mass is negligible, so F only has to compress and extend the spring. So in that limit, applied force F = +kx. (The spring force is –kx.) The mechanical impedance of the system at this low frequency is compliant or spring-like. Acoustically, it looks like an acoustic compliance: we push the mass of air in the neck and compress the air in the resonator. The applied force F to the right is in phase with x measured to the right, so it is 90° behind the velocity and the applied pressure is 90° behind the acoustic flow into the resonator.

Remember that f² dependence of the acceleration. So, at sufficiently high frequency, the spring force is negligible in comparison with that accelerating the mass. So F is in phase with the acceleration, which puts it 90° ahead of the velocity. Acoustically, the applied pressure is 90° ahead of the acoustic flow into the resonator. It is a mechanical or acoustic inertance.

At the resonant frequency (still talking about the sketch above), the amplitude can be large for very small force. So at resonance, the impedance is very low, when viewed from force applied to the mass from outside (the diagram above). At resonance, there is maximum flow into and out of the resonator.

Now consider what happens if we look at the pressure inside the resonator (away from the neck). Here we are looking at the force on the spring, so our mechanical analogue looks like this schematic.

circuit diagram of Helmholtz resonance

This time, low frequency means that the force can be small for a given amplitude: the spring and mass move together as a mass, and the system this time looks inertive at low frequency. At high frequency, the mass hardly moves, and the system is spring-like or compliant. So the phase relations are opposite to what we had before: at low f, p leads U by 90°; at high f, p lags U by 90°. At low frequency, the pressure inside the bottle accelerates that vibrating mass of air , so from the inside it is an acoustic inertance. At high frequency, the mass of air doesn't have time to move, so any driving oscillation inside the bottle must compress the air, which means it sees an acoustic compliance.

Complications involving the effective length

The first diagram on this page draws the 'plug' of air as though it were a cylinder that terminates neatly at either end of the neck of the bottle. This is oversimplified. In practice, an extra volume both inside and outside moves with the air in the neck – as suggested in the animation above. The extra length that should be added to the geometrical length of the neck is typically (and very approximately) of 0.6 times the radius at the outside end, and one radius at the inside end).

An example. Ra Inta made this example. He took a spherical Helmholtz resonator with a volume of 0.00292 m³ and a cylindrical neck with length 0.080 m�and cross-sectional area 0.00083 m². To excite it, he struck it with the palm of his hand and then released it. A microphone inside the resonator records the sound, which is shown in the oscillogram at left. You can see that the hand seals the resonator for rather less than 0.1 s, and that during this time the oscillations are weaker and of relatively high frequency.

Once the hand is released, an oscillation is established, which gradually dies away as it loses energy through viscous and turbulent drag, and also by sound radiation. Close examination shows that the frequency rises slightly as the hand moves away from the open end, because this the hand restricts the solid angle available for radiation and thus increases the end effect (or end correction).

The length of the neck is increased by one baffled and one unbaffled end effect, giving it an effective length of 0.105 m. With a speed of sound of 343 m/s, the expression above gives a resonant frequency of 90 Hz.

Sound of the resonator being slapped.

Waveform

Waveform (top) and sound spectrum (the latter on a log-log scale) of the impact response of a Helmholtz resonator.

Helmholtz resonances and guitars

* I said above that the air in the body of a guitar acts almost like a Helmholtz oscillator. This case is complicated because the body can swell a little when the air pressure rises inside – and also because the air 'in' the sound hole of the guitar has a geometry that is less easily visualised than that in the neck of a bottle. Indeed, in the case of the guitar body, the length of the plug of the air is approximately equal to the two 'end effects' at the end of a 'pipe' which is only a couple of mm thick. The end effects, however, are related to and of similar size to the radius of the hole, so the mass of air is substantial. The length of the end effect of a cylindrical pipe that opens onto an infinite, plane baffle is 0.85 times the radius of the pipe. Although the soundboard of a guitar is not infinite, one would expect a similar end effect, and so the effective length of the 'plug' of air would be about 1.7 times the radius of the hole. (Some makers increase this by fixing a short tube below the soundhole, with equal radius.)

A couple of people have written asking how big the sound hole should be for a given instrument. Well, we can use the equation above to start to answer that question. However, the swelling of the body is important. This makes the 'spring' of the air rather softer, and so lowers the frequency. The purely Helmholtz resonance can be investigated by keeping the body volume constant. When measuring this, a common practice is to bury the guitar in sand, to impede the swelling or 'breathing' of the body. However, guitars are not usually played in this situation. So the Helmholtz calculation will give an overestimate of the frequency of resonance for a real, flexible body.

Let's assume a circular sound hole with radius r, so S = πr², and L = 1.7r as explained above. When we substitute into the equation for the Helmholtz frequency, using c = 340 m/s, we get: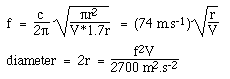

Notice that we are using standard SI units: we have used the speed of sound in metres and seconds, so the volume must be in cubic metres and the frequency in Hertz, to give an answer in metres.

It is more complicated when the tone holes are not circular, because the end effect is not equal to that of a circle with the same area. PhD student and luthier John McLennan is writing up a report of some measurements about this, which we'll post here soon.

On guitar and violin family instruments, the Helmholtz (plus body) resonance is often near or a little below the frequency of the second lowest string, around D on a violin or G-A on a guitar. You can reduce or shift the Helmholtz frequency substantially by covering all or part of the hole with a suitably shaped pieced of stiff cardboard. If you then play a note near the resonance and then slide the card so it alternately covers and reveals the hole, you'll clearly hear the effect of the resonance.

Is the 0.85r effect reasonable? Ra Inta, who did a PhD on guitar acoustics in our lab, suggests an interesting demonstration:
Damp the strings on your guitar so they don't vibrate (e.g. a handkerchief between strings and fingerboard). Hold the palm of one hand above the soundhole, and close to it. With a finger of your other hand, strike the soundboard a sharp blow near the soundhole and close to the 1st string. You will feel a pulse of air on the palm of your hand. The blow of your finger pushes the soundboard in and squeezes some air out of the body. Now move your hand gradually further away from the hole, and continue tapping with the finger. When do you cease to feel the movement of the air? This will give you a rough estimate of the length of the 'end effect' in the case of the sound hole.

Tuning the Helmholtz resonance

Among the publications of John McLennan, a PhD student in this lab, is an article in which he varies the Helmholtz resonance by varying the speed of sound.

McLennan, J.E. (2003) "A0 and A1 studies on the violin using CO₂, He, and air/helium mixtures." Acustica, 89, 176-180.