The Mandelbrot set is a fascinating example of a fractal complexity that can be generated from a very simple equation: z = z*z + c. Here is a program to generate an image of the Mandelbrot set:
/*
A program to generate an image of the Mandelbrot set.
Usage: ./mandelbrot > output
where "output" will be a binary image, 1 byte per pixel
The program will print instructions on stderr as to how to
process the output to produce a JPG file.
Michael Ashley / UNSW / 13-Mar-2003
*/
// Define the range in x and y here:
const double yMin = -1.0;
const double yMax = +1.0;
const double xMin = -2.0;
const double xMax = +0.5;
// And here is the resolution:
const double dxy = 0.005;
#include <stdio.h>
#include <limits.h>
int main(void) {
double cx, cy;
double zx, zy, new_zx;
unsigned char n;
int nx, ny;
// The Mandelbrot calculation is to iterate the equation
// z = z*z + c, where z and c are complex numbers, z is initially
// zero, and c is the coordinate of the point being tested. If
// the magnitude of z remains less than 2 for ever, then the point
// c is in the Mandelbrot set. We write out the number of iterations
// before the magnitude of z exceeds 2, or UCHAR_MAX, whichever is
// smaller.
for (cy = yMin; cy < yMax; cy += dxy) {
for (cx = xMin; cx < xMax; cx += dxy) {
zx = 0.0;
zy = 0.0;
n = 0;
while ((zx*zx + zy*zy < 4.0) && (n != UCHAR_MAX)) {
new_zx = zx*zx - zy*zy + cx;
zy = 2.0*zx*zy + cy;
zx = new_zx;
n++;
}
write (1, &n, sizeof(n)); // Write the result to stdout
}
}
// Now calculate the image dimensions. We use exactly the same
// for loops as above, to guard against any potential rounding errors.
nx = 0;
ny = 0;
for (cx = xMin; cx < xMax; cx += dxy) {
nx++;
}
for (cy = yMin; cy < yMax; cy += dxy) {
ny++;
}
fprintf (stderr, "To process the image: convert -depth 8 -size %dx%d gray:output out.jpg\n",
nx, ny);
return 0;
}
If you enjoyed that, have a look for the program "fracint" for Windows machines, and "mxp" for GNU/Linux. Here are some examples from "mxp", showing the complete Mandelbrot set first, and then enlargements of various sections of it:
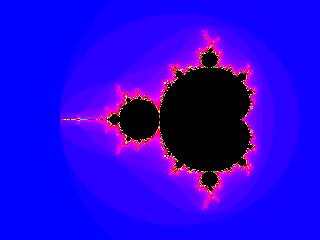



The following is an improved version of the above program, using integer arithmetic in the "for" loop, to guarantee the size of the image.
/*And here is a version using the C-99 complex numbers:
A program to generate an image of the Mandelbrot set.
Usage: ./mandelbrot > output
where "output" will be a binary image, 1 byte per pixel
The program will print instructions on stderr as to how to
process the output to produce a JPG file.
Michael Ashley / UNSW / 13-Mar-2003
*/
const double xCentre = -0.75;
const double yCentre = +0.0;
const int nx = 400;
const int ny = 400;
const double dxy = 0.005;
#include <stdio.h>
#include <limits.h>
int main() {
double cx, cy;
double zx, zy, new_zx;
unsigned char n;
int i, j;
// The Mandelbrot calculation is to iterate the equation
// z = z*z + c, where z and c are complex numbers, z is initially
// zero, and c is the coordinate of the point being tested. If
// the magnitude of z remains less than 2 for ever, then the point
// c is in the Mandelbrot set. We write out the number of iterations
// before the magnitude of z exceeds 2, or UCHAR_MAX, whichever is
// smaller.
for (j = 0; j < ny; j++) {
cy = yCentre + (j - ny/2)*dxy;
for (i = 0; i < nx; i++) {
cx = xCentre + (i - nx/2)*dxy;
zx = 0.0;
zy = 0.0;
n = 0;
while ((zx*zx + zy*zy < 4.0) && (n != UCHAR_MAX)) {
new_zx = zx*zx - zy*zy + cx;
zy = 2.0*zx*zy + cy;
zx = new_zx;
n++;
}
write (1, &n, sizeof(n)); // Write the result to stdout
}
}
fprintf (stderr, "To process the image: convert -depth 8 -size %dx%d gray:output out.jpg\n",
nx, ny);
return 0;
}
/*
A program to generate an image of the Mandelbrot set.
Usage: ./mandelbrot > output
where "output" will be a binary image, 1 byte per pixel
The program will print instructions on stderr as to how to
process the output to produce a JPG file.
Michael Ashley / UNSW / 23-Apr-2004
*/
const double xCentre = -0.75;
const double yCentre = +0.0;
const int nx = 400;
const int ny = 400;
const double dxy = 0.005;
#include <stdio.h>
#include <unistd.h>
#include <limits.h>
#include <complex.h>
int main() {
double complex c, z;
unsigned char n;
int i, j;
// The Mandelbrot calculation is to iterate the equation
// z = z*z + c, where z and c are complex numbers, z is initially
// zero, and c is the coordinate of the point being tested. If
// the magnitude of z remains less than 2 for ever, then the point
// c is in the Mandelbrot set. We write out the number of iterations
// before the magnitude of z exceeds 2, or UCHAR_MAX, whichever is
// smaller.
for (j = 0; j < ny; j++) {
for (i = 0; i < nx; i++) {
c = xCentre + (i - nx/2)*dxy + I * (yCentre + (j - ny/2)*dxy);
z = 0.0;
n = 0;
while ((cabs(z) < 2.0) && (n != UCHAR_MAX)) {
z = z*z + c;
n++;
}
write(1, &n, sizeof(n)); // Write the result to stdout
}
}
fprintf (stderr, "To process the image: convert -depth 8 -size %dx%d gray:output out.jpg\n",
nx, ny);
return 0;
}