1D cellular automata - image output

// Cellular automata
// Wolfram, "A New Kind of Science", Chapter 2 and 3.

// Michael Ashley / UNSW / 11-May-2003

#define displayWidth 640
#define maxSteps     480

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <unistd.h>

/*
  Each cell has a value of 0 or 1.

  The value of a cell in the next generation depends on its current
  value, and the values of the neighbouring two cells. 

  The calculation of the new value therefore depends on the values of 
  3 single-bit quantities, giving 8 possible alternative configurations.

  The calculation can therefore be represented using a array giving the
  8 possibilities. We call this array "rule".
*/

int rule[8];

typedef struct {
	unsigned char cell[displayWidth + 2 * maxSteps];
} state;

void initialise(state * s) {
	int i;
	for (i = 0; i < (sizeof s->cell) / (sizeof s->cell[0]); i++) {
		s->cell[i] = 0;
		if (i == maxSteps + displayWidth / 2)
			s->cell[i] = 1;
	}
}

void createRule(int r[8], unsigned char n) {
	int i;
	for (i = 0; i < 8; i++) {
		r[i] = 0x01 & (n >> i);
	}
}

void applyRule(state * prev, state * next, int i) {

	/* This function takes an existing state, prev, and applies the
	   evolution rule to the i'th element, returning the result in next. */

	next->cell[i] = rule[prev->cell[i - 1] * 4 +
                        prev->cell[i] * 2 + 
                        prev->cell[i + 1]];
}

void evolve(state * prev, state * next) {

	/* Applies the rule to all elements (apart from the end-points) of
	   an existing state, prev, and returns the result in next. */

	int i;
	for (i = 1; i < (sizeof prev->cell) / (sizeof prev->cell[0]) - 1; i++) {
		applyRule(prev, next, i);
	}
}

void displayState(state * s) {
        assert(displayWidth == write(1, &s->cell[maxSteps], displayWidth));
}

void usage(char *prog) {
 	printf("Usage: %s rule | display -size %dx%d -depth 1 gray:-
    where rule is an integer between 0 and 255 inclusive\n", 
    prog, displayWidth, maxSteps);
	exit(1);
}

int main(int argc, char **argv) {
	int n, i;
	state s0, s1;

	assert(maxSteps % 2 == 0); // Ensure we have an even number of steps.

	initialise(&s0);
	initialise(&s1);

	if (argc != 2 || 
	    1 != sscanf(argv[1], "%d", &n) || 
            n < 0 || 
            n > 255)
		usage(argv[0]);

	createRule(rule, n);

	for (i = 0; i < maxSteps / 2; i++) {
		displayState(&s0);
		evolve(&s0, &s1);
		displayState(&s1);
		evolve(&s1, &s0);
	}
	return 0;
}

Interesting features of this program include:

• The usage message describes how to run the program to produce an image display (assuming the availability of the ImageMagick software).
• The fact that it was easily created by simple modifications of the text-output version.

And here are some examples of the output from this program:

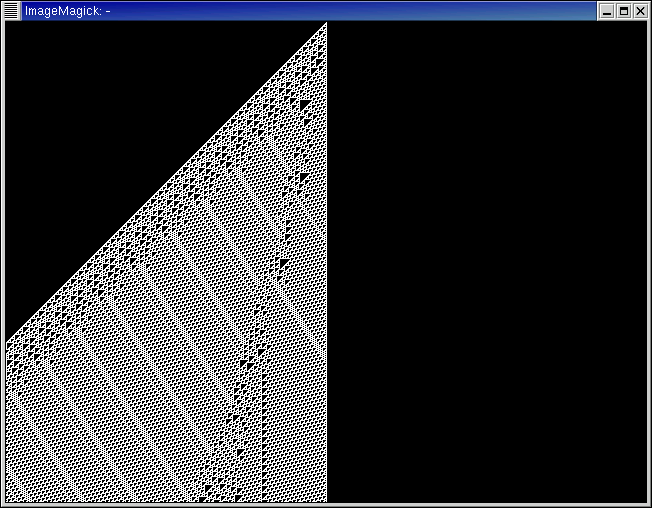
Rule 2, a class 1 cellular automata

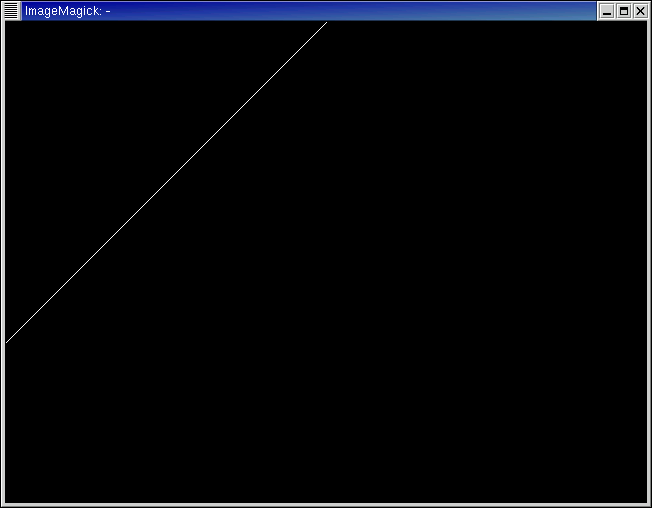
Rule 22, a class 2 cellular automata

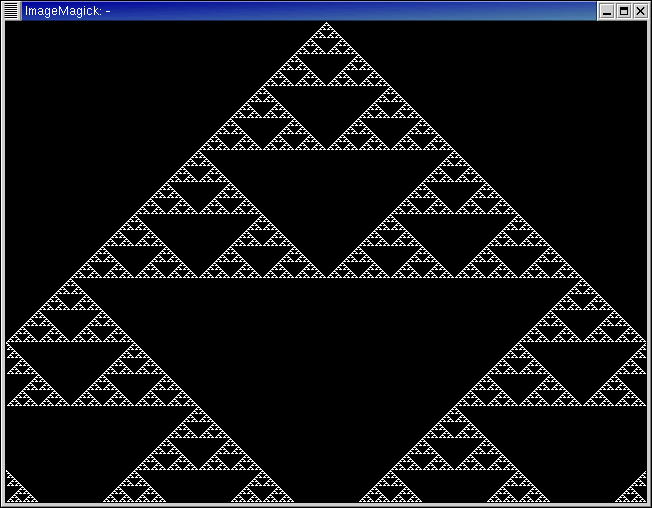
Rule 30, a class 3 cellular automata

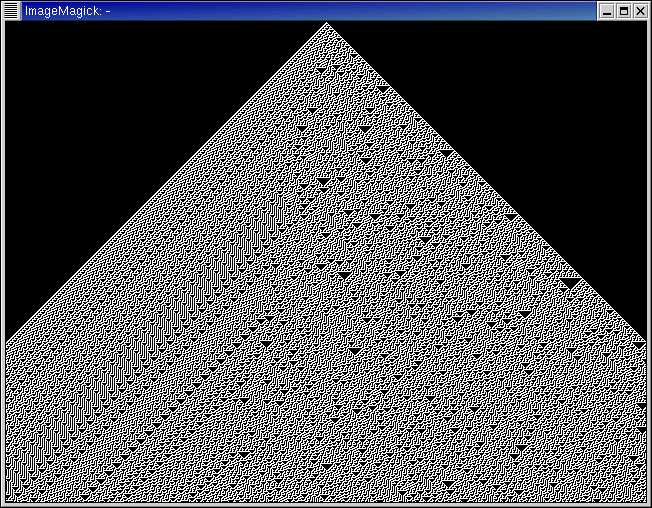
Rule 110, a class 4 cellular automata