|
|
|
|
The physics of sailingSailing gives examples of physics: Newton's laws, vector subtraction, Archimedes' principle and others. This support page from Physclips asks
A puzzle. A river runs straight from West to East at 10 knots. A 10 mile race is held: the boats sail downstream, from West to East. The first heat is held in the morning, when there is no wind. The second heat is held in the afternoon, when there is a 10 knot wind from the West. In which heat are the faster times recorded? (Answer below.)
|
|
Sailing downwind (parallel to the wind, like the boat at left) is easy to understand: the wind blows into the sails and pushes against them. For a boat sailing directly downwind, the wind is faster than the boat so the air is decelerated by the sails. So the wind pushes forward on the sails but the sails push backwards against the wind - Newton's third law. But for a boat with normal sails, the catch is that, downwind, you can only ever sail more slowly than the wind, even with a spinnaker. Which is comfortable, but not the most interesting sailing.
You're already familiar with the wind force: In a strong wind, it is easier to walk, run or bicycle with the wind pushing on your back. Usually, the wind pushes you in the direction it is going. Sailing directly upwind (exactly anti-parallel to the wind, like the boat at right) is also easy to understand: it's impossible (impossible with sails: a boat with a wind turbine driving a propellor could go directly upwind. ). You just sit there with your sails flapping. This is also not interesting sailing. But boats can sail at say 40° to the wind and, by tacking (sailing courses alternately to the left and right of the direction of the oncoming wind) they can go where they like. So let's think about.... |
|
|
An experiment. Here is what my left hand looks like as I bicycle, signalling a left turn. If my hand is flat and horizontal, I just feel the drag force of the wind acting backwards. But if I tilt my hand up a little at the front, I feel lift force as well: the force on my hand is both upwards and backwards. The arrows show the wind speed relative to me. To get past my hand, the wind is deflected down, and this pushes my hand up (as well as back). In this diagram, the quantities force and velocity have arrows, because they have a magnitude as well as a direction. Try this link for an Introduction to vectors. |
|
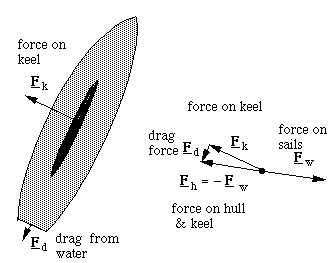
 Sailing close to the wind uses the shape of the sails to generate lift. To flow around the sails, the wind has to deviate in direction, as shown by the arrows for initial velocity vi and final velocity vf, which are given with respect to the boat. The change of velocity dv is in the direction shown. The acceleration aa of the air is dv/dt, so the force Fa that sails exert on the air is in the same direction. (Newton's first and second laws: F = ma.) The force Fw that the wind exerts on the sails is in the opposite direction. (There is also a Bernoulli effect, which contributes in a secondary way.)
Sailing close to the wind uses the shape of the sails to generate lift. To flow around the sails, the wind has to deviate in direction, as shown by the arrows for initial velocity vi and final velocity vf, which are given with respect to the boat. The change of velocity dv is in the direction shown. The acceleration aa of the air is dv/dt, so the force Fa that sails exert on the air is in the same direction. (Newton's first and second laws: F = ma.) The force Fw that the wind exerts on the sails is in the opposite direction. (There is also a Bernoulli effect, which contributes in a secondary way.)Note that nowhere in this argument did we need to say that the wind was faster than the boat. Now this force is mainly sideways on the boat, and it gets more and more sideways as you get closer to the wind. However, part of the force is forward: the direction we want to go. So... Why doesn't the boat drift sideways? Well it does a little, but when it does, the keel (a large nearly flat, nearly vertical area under the boat) has to push a lot of water sideways. The water resists this, and exerts the sideways force Fk on the keel.
This cancels the sideways component of Fw. As to the forwards component: it accelerates the boat until the drag force Fd holding it back is big enough so that
|
|
How can boats sail faster than the wind? Lots of boats can – including the eighteen footer skiffs on Sydney Harbour. Ask a sailor how, and he'll say "These boats are so fast that they make their own wind", which is actually true. Ask a physicist, and she'll say that it's just a question of vectors and relative velocities.
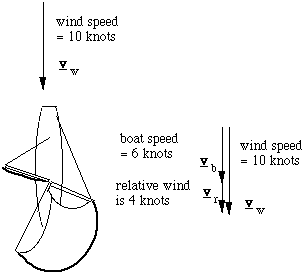
Downwind (diagram at left) is easy. If the wind is 10 kt, and the boat makes 6 kt in the same direction, then the crew feels a wind of 4 kt coming over the stern of the boat. The true wind vw equals the speed of the boat vb plus the relative wind vr. The equation vw = vb + vr tells us the problem: as the boat speed approaches the wind speed, the relative wind drops towards zero and so there is no force on the sail. So you can't go faster than the wind. When the wind is at an angle, we have to add the arrows representing these velocities (vector addition). Upwind (right), exactly the same equation holds: vw = vb + vr.
The faster that the boat goes, the greater the relative wind, the more force there is on the sails, so the greater the force dragging the boat forwards. So the boat accelerates until the drag from the water balances the forward component of the force from the sails.
|
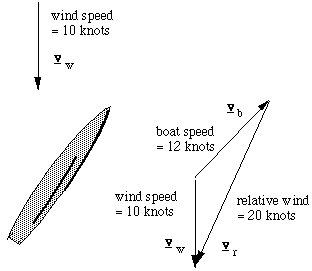
Why are eighteen foot skiffs always sailing upwind? In a fast boat, there's no point going straight downwind: you can never go faster than the wind. So you travel at an angle. But if your boat is fast enough, then the relative wind always seems to be coming mainly from ahead of you, as these arrows show. So the eighteen footers never set ordinary spinnakers: they have asymmetrical sails that they can set even when they are travelling at small angles to the apparent wind.
|
|
Links
Answer to puzzle. The faster heat is the one with no wind. When the wind and the water both move W to E at 10 kt, the boats drift down the river at 10 kt, with their sails hanging limp. In the heat with no wind (as measured on the land), a drifting boat has a headwind of 10 kt. You can tack into that. Of course, you don't get something for nothing. In the heat with wind, the river does very little work on the boat. In the heat without wind, it exerts much greater force on the boat, in particular on the keel or centreboard. Much of that work goes into disturbing the air downwind of the boat's sails. Tricky? The man in the photo at right did a lot of sailing on rivers: he would have known that. |
|
|
Joe
Wolfe sails a classic sloop called Inala of Huon
© 2002. Modified 10 Jan 03 J.Wolfe@unsw.edu.au, phone 61-
2-9385 4954 (UT + 10, +11 Oct-Mar).
|
|