A recipe for a violin
J. E. McLennan
Violin making up to the beginning of the 19th century could be described as a craft. For success a craft has to follow a strict recipe which is arrived at by trial and error and the venture into small variations in practice and noting the resultant effect with the benefit of adoption if an improvement occurs. The craft of blacksmithing followed by a similar process. The production of hardened blades whether in Toledo or Damascus required much experimentation. In both cases, it was not until the craft was mastered and producing the finest articles that the understanding of the underlying principles began to be investigated. In the case of the metallurgy behind the blacksmith's art, once understood, a world of opportunity was opened up due to the wide variety of metals and alloys. This was not possible with the craft of violin making having chosen the best materials very early. Subsequent attempts with new materials have been limited for aesthetic reasons.
Following the study of string behaviour by Pythagoras and Mersenne, the scientific study of the violin can be regarded as beginning with Felix Savart early in the 19th century. From then on, with a burst in the 1930s, the acoustics of the violin has received extensive treatment.
Understanding the way a violin converts the playing action of the bow on the strings into radiated sound has reached the point where some guidelines can be given to maximise response and sound output. Studies have concentrated on the response expressed in the form of a plot of output sound level in dB against frequency from typically 200 Hz to 10 kHz, often measured a microphone a short distance in front of the top plate. Another plot that is easy to obtain is the input admittance at the top of the bridge. In both cases, the strings are damped to exclude string resonances and the violin is excited by an impact hammer strike at the top of the bridge. The velocity (obtained using a small magnet and coil) or the sound pressure are analsyed using a DFT program readily available on computers.
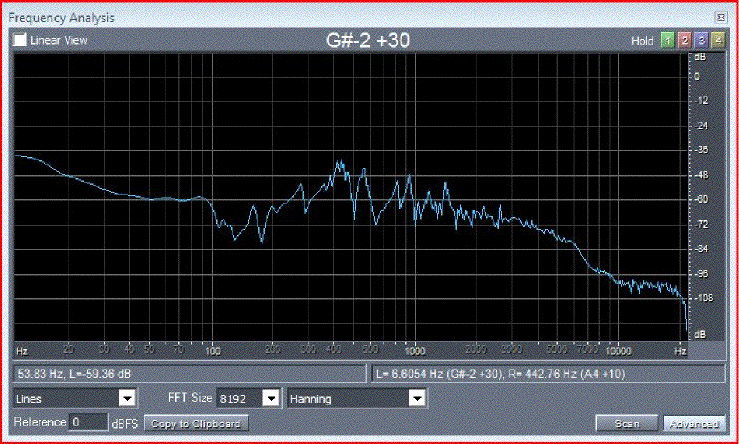 |
Figure 1a. Tap response plot showing input admittance at the top of the bridge. At 300 Hz A0 peak and Helmholtz dip are visible. At 500 Hz the trough between the main body modes, B1- and B1+ is shown. Other body peaks are shown.
Figure 1b. Tap response plot showing microphone response. A0 at 285 Hz and body modes B1- at 424 Hz, A1 at 485 Hz and B1+ at 560 Hz with the trough at 500 Hz. No trough above A0. The response is raised at 2000 Hz by the bridge effect.
The plot obtained in this way shows all the resonance peaks possessed by the violin that has responded to the excitation. The peaks below 1 kHz are separated sufficiently that their mode shapes can be studied simply by irradiation with a single frequency over a speaker using e.g. tea leaves to delineate the nodal lines. The form of the response plot shows the relative level of the peaks and their frequency. The plot also shows the polarity of resonance, the two main body modes at about 500 Hz have positive polarity which results in a deep trough between them. The main air resonance, the peak with the lowest frequency, behaves with negative polarity as there is no trough between it and the next higher peak. A positive polarity is defined as an increase in air volume when the bridge moves to the right. If the air volume decreases the polarity is negative. Two adjacent body peaks with the same polarity will have a trough between them. Beside the relative strength and mode shape of a resonance, its Q value, effective mass and stiffness can be measured. From these parameters the radiation resistance can be calculated; a low value indicating a good radiator. A good radiator implies a high monopole component, or breathing mode, in the resonance. The monopole component is probably linked with good projection from the instrument and is important below 1 kHz where most fundamentals occur.
The Main Air Resonance
A strong main air resonance with a low radiation resistance and Q value of about 10, is important. It is composed entirely of a monopole and its radiation resistance will be lowered by a low mass, flexible body. The soundpost can reduce the size of the “island” by being outside the treble foot of the bridge. For the size of f holes in use and considered aesthetically pleasing, the volume of air to give A0 at about 275 Hz is 2 litres with the existing plate size, the sides come out at 30 mm and the arch height at 15 mm. There are higher air modes but it is not known what effect they have. The first higher air mode at 485 Hz is not a strong radiator.
Body Resonances
There are a number of body resonances between 385 Hz and 900 Hz. They have been identified and well documented. It is possible to obtain the parameters of each resonance as outlined above to give the Q value and the radiation resistance. A Q value of about 50 appears to be ideal and should lower the risk of wolf notes.
A0 285 Hz C2 385 Hz B1- 422 Hz B1+ 528 Hz C4 600 Hz ? 852 Hz
Figure 2. Chladni patterns for Violin No 3, modern setup, showing body resonances, above the top and below the back of the violin. The air mode, extreme left, is not body resonance in the same sense as the others.
Nodal patterns become more complex as the frequency is raised and above 1 kHz plate modes become important. The radiation becomes more directional at these higher frequencies. For all resonances nodal lines should be thin and for body modes placed to maximise the monopole component for good projection and maximum output.
The body resonances will depend for their properties on the behaviour of the plates. The free plate vibrations have been studied extensively but no correlation has been found with the frequencies of the body resonances. The presence of thin nodal lines, their wide placement and a large amplitude of vibration have been aimed at when thicknessing the plates. An octave between the three main modes in the top with mode 1 not less than 90 Hz have been easily obtained. Cutting the soundholes has the effect of lowering the frequency of mode 5 by about 60 Hz without affecting modes 1 and 2 and which can be restored by thinning the bassbar. The bassbar can be used to vary the frequency of mode 5. While the top is thinned uniformly to about 3 mm, the back is thicknessed differently. The central region is usually about 4 mm reducing to 2.5 mm at the margins. Unlike other instruments where the sides and back with an amplitude less than that of the top, can be regarded as forming a support for the top as the active membrane, the soundpost brings the back into action. The accepted wisdom was to keep the mode frequencies high and match mode 2 in both back and top. There might be a case for lowering mode 5 in the top with a thinner bassbar to achieve a lower mass while preserving sufficient strength to resist the stress of fitting up. A full arch without any channel would help in this regard.



Figure 3. Chladni patterns for violin No 3, of free plate mode for the top above without and with bassbar and the back plate below. Modes 1, 2 and 5 are shown from left the right.
The body of the violin is the result of gluing a top and back plate onto an assembled rib structure. I prefer to have the ribs and neck assembled allowing for the overstand and leaving the shoulder projecting where the button will be finally glued. The overstand and the neck angle should be set to give a bridge height of 35 mm. I like to glue the top onto the ribs first so that the neck and fingerboard, which can be temporarily glued in place, is able to be accurately lined up with the f-holes. The back is attached last after the ribs are tapered from the top corners to the button about 2 – 3 mm. The back is first glued from the top block to the top corners and then sprung to glue onto the rest of the rib assembly. This will put the plates in tension.
The Bridge Function
The bridge has an important role in raising the response between 2 and 3 kHz. The first resonance of the bridge occurs in this range on the violin. This bridge/body hill effect has a radiation resistance of about 5 which makes it a good radiator for the harmonics in the sound. The response of the violin falls off at about 5 kHz. The bridge resonance operates in the region of the harmonics to most notes and in which plate resonances are active. The radiation is more directional at these high frequencies.
Discussion
The general design of the violin has to be similar to the classical form, if not taken directly from an actual classical instrument. The reason for this is the appearance and attractive proportions that culminated with the style used by Andrea Amati in the 16th century. There has been no serious attempt to depart from this.
The total mass of the violin is an important factor. This is associated with the construction of the body is the source of the sound radiation. Thin ribs, about 1 mm thick, and tapered linings and rounded blocks indicate the methods used by past makers. High quality tone wood and attention to the optimum arching and plate thicknesses are essential to a fine instrument. The use of scrapers for the finish of all surfaces, the use of a sealer, possibly Cera Colla, and an oil varnish to enhance the beauty of the wood are all important aspects.
The main objective of the maker is a high output, ease of playing and good projection. One has to keep in mind the overall picture e.g. that the force exerted by the player is less than one hundredth of the forces existing in the tuned instrument.
It might be possible to construct a computer model to study the influence of nodal line position for the main resonances below 1 kHz, as affected by the arching on the monopole content. This may well be the controlling factor in the projection of the violin.
Further reading
| 