Acoustic impedance for the lowest note

Acoustic impedance for the lowest note on the flute

note C4

new window for C4

What is acoustic impedance?

The impedance spectrum for C4 on a C foot flute

For this case, the flute most closely approximates a simple cylindrical pipe, open at the far end, which is a standard case considered in textbooks about acoustics. (There are differences, of course: the closed tone holes each have a little volume added to the side of the bore; the head joint of the flute is not cylindrical but tapered to a smaller diameter near the embouchure hole and we are driving it at the embouchure hole which is, in effect, a little side tube some distance from the end of the pipe.)

The impedance spectrum shows a regular series of maxima and minima. These correspond to the resonances of the flute (or pipe) in this configuration. The minima correspond to resonances for the condition when the embouchure end is open (like a flute) while the maxima are resonances for the condition when the embouchure end is closed (like a clarinet - see Flutes vs Clarinets).

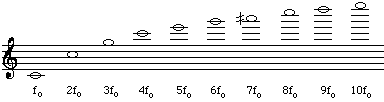
With this fingering, the flute will play a series of notes at frequencies near to the minima in this spectrum. Keeping all the keys closed, and just by blowing harder and adjusting the embouchure one can play at least the first 7 or 8 notes in the harmonic series, as shown below (Note the half sharp - the seventh note in the series is between A6 and A#6, slightly closer to the latter.)

As is the case for a simple cylindrical pipe, the amplitude of the maxima and minima decreases with frequency - you will have noticed that the notes get harder and harder to play as you go up. This is due to viscous losses. The air flow is greatest in the centre of the flute, and zero at the walls. Some energy is lost in overcoming the viscous drag of the air, and this limits the sharpness (lowers the Q factor) of the resonances. The effect is greater for high frequencies.

Note that the maxima and minima are not symmetric. The minima occur at frequencies lower than halfway between the maxima, particularly at high frequencies. This feature is not observed in the impedance of a simple cylindrical pipe, and may be qualitatively explained as follows: One difference between a flute and the simple cylinder of acoustics textbooks is that the embouchure hole of the flute is displaced from the end, and it is smaller in diameter than is the flute. This reduction in diameter is expected to have relatively little effect on the impedance maxima, where there is almost no flow and so the obstruction has little effect. It has rather a greater effect on the impedance minima, where flow is high and the pressure is low. This obstruction slows the vibration and the minima are flattened with respect to the maxima. In fact flutists use this obstruction effect to keep the instrument in tune: in order to play a note flatter, they roll the flute towards them, so that the embouchure hole is more occluded.

For more detail, see What is acoustic impedance and why is it important?, and Introduction to flute acoustics. See also Acoustic impedance of classical and modern flutes, and this excellent reference book: Fletcher, NH and Rossing, TD (1998) "The Physics of Musical Instruments" Springer-Verlag, New York.