|
|
|
| Relativity
in brief... or in detail.. |
The Planck scale: relativity meets quantum mechanics meets gravity.
Does Planck-scale physics challenge relativity? According to Special Relativity's time dilation and length contraction, two observers with relative motion are condemned to eternal disagreement about times and lengths. Or are they? They will disagree over the arbitrary times measured in seconds and lengths measured in metres. They would also disagree over clock ticks, atomic vibrations and light wavelengths. But what if there were some absolute time and length, determined by the very nature of the universe? And what if these quantities could be measured in different frames of reference? Wouldn't the observers have to agree on those having the same value, if they agree on the same laws of physics? Well, there is an abolute length and an absolute time. It's possible that we'll never be able to measure them, so any threat posed to relativity is distant and perhaps even hypothetical. It is interesting to see whether and how these quantities might be included in relativity.
Combining quantum mechanics, gravity and relativitySo, where do the Planck scale quantities come from? The speed of light c is the natural unit that relates time and space. G is the constant of gravity, and h is Planck's constant, which comes from quantum mechanics. So the Planck scale becomes involved when we combine gravity, quantum mechanics, time and space. Currently, we don't know much about this interaction, because gravity is so weak that its influence on things as small as quantum systems is immeasurably small — or alternatively we could say that quantum effects are immeasurably small for objects (such as planets) that are large enough to have substantial gravitational effects.Special Relativity and quantum mechanics work very well together. Indeed, relativistic quantum electrodynamics is a spectacularly accurate theory. Richard Feynman once described how accurate it was by saying: 'It's as though you asked me how far it was to the moon and I said "do you mean from my head or from my feet?".' And it's now more accurate than when he said that. This diagram shows the combinations. 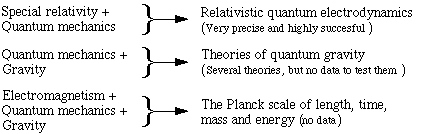 What do space and time mean at the Planck scale?Quantum mechanics and gravity (whether Newton's theory of gravity or Einstein's theory of General Relativity) do not fit so neatly together. The problem can be put in several different ways, but I favour this one. From our discussion of virtual particles (Why there would be no chemistry without relativity), we saw that virtual particles could be more massive if their lifetime and range were smaller.Now both Newton's and Einstein's gravity predict that enough mass in a small enough space can produce a black hole: a region with a gravitational field so strong that its escape velocity is greater than c. When we put the two ideas together, we find that there is a scale small enough for virtual black holes to exist. This is the Planck scale. On this scale, a black hole can appear spontaneously ó but very briefly ó anywhere in space. So, examined on this scale, all of the weird, singular behaviour associated with black holes asserts itself, not just in remote astrophysical peculiarities, but everywhere and at all times. With black holes winking in and out of existence everywhere at once, space and time as continuous entities cease to have meanings when discussing distances of 10-35 metres and times of 10-44 seconds. So relativity, a classical theory of space and time based on a space-time continuum, might run into serious difficulties. Which is perhaps not surprising: the Planck scale is a very, very long extrapolation from our current knowledge. And from our current cosmological era. The Planck epoch and the early universe.For all time, the universe has been expanding. If we imagine reversing this and extrapolate back to the very early universe, we arrive at the Planck epoch, a time when the temperature was ~TP, so particle energies were ~EP (see above) and Planck scale phenomena dominate. It is thought that all four forces (strong, weak, electromagnetic and gravity) were combined in one unified force. We donít have a convincing quantum theory of gravity yet and we canít apply General Relativity to the Planck epoch. However, the Uncertainty Principle (see above) implies that, in the Planck epoch, black holes spontaneously appear and disappear everywhere.What was the age of the universe when its temperature was ~TP (i.e. 1.4 x 1032 kelvins)? It's tempting to say that the universe's age was ~tP (= 5.4 x 10-44 seconds), measured starting from a t = 0 singularity which had infinite temperature and density. But physicists are reluctant to admit infinities. Further, at Planck temperatures and above, with black holes appearing and disappearing everywhere all at once, time and space don't have their usual meaning and possibly no meaning at all. (And perhaps cause and effect don't have meaning either, which would be one way of dodging the question about the origin of the universe.) On the Planck scale, we have so little direct knowledge that there are few hints to guide the development of theories, and few constraints upon those theories. Currently, there are several different families of theories that aim to produce a consistent theory of quantum gravity. Some include a larger number of spatial dimensions, not all of which are macroscopic*. At the moment, however interesting they be, these theories are speculative. Perhaps one of them will turn out to be a good, useful theory, and the others will fall. At the moment, we cannot put them to the test. Here's an analogy. Today, we remember Democritus for speculating on the existence of atoms. But the ancient Greek philosophers proposed so many ideas that it is not too surprising that some of them turned out to be consistent with facts determined much later. Meanwhile, here are a couple of our pages that may interest you:
* How can we have more than three spatial dimensions? Surely Gauss' law (for electricity, magnetism and gravity) shows that we live in a locally flat geometry with three spatial dimensions? Yes, experiments to test Gauss' law for electricity either directly or indirectly do show that our geometry is both very flat and three dimensional on the scale of the experiments conducted. If, however, the universe were closed in all but three of the spatial dimensions, and if, in the closed dimensions, the radius of the universe were much smaller than the size of measurements (say less than the dimensions of fundamental particles), then Gauss' law would apply only to the three large dimensions — a Gaussian surface would never intersect one of the closed dimensions. Consequently electricity, magnetism and gravity would be inverse square laws on the scales that are experimentally accessible. The theories that use extra dimensions then have the possibility to use such ideas as representing particles as standing waves on the circumference of the universe in the closed dimensions. |
Home
| Summary
| Quiz
|
Credits
|
|