|
|
|
| Relativity
in brief... or in detail.. |
The Lorentz transform equations, the addition of velocities and spacetime
Galilean transform equationsIn An introduction to the mechanics of Galileo and Newton, we saw that converting between two inertial frames was easy in that version of mechanics. Let's consider motion in the x direction, with relative speed v: the train goes past the station at v (on a straight and level track that we call the x axis). We synchronise watches (set t = 0) at some convenient time, let's say when the back of the train passes Jasper, the observer in the station. So the position of the back of the train is x = vt, where t is the time elapsed. If Zoe, a passenger in the train, is a distance x' ahead of the back of the train, then Jasper sees her position as x = vt + x', where we use the prime (') to signify Zoe's frame and the absence of it to signify Jasper's.Formally, we should consider the y and z directions too. In Galilean relativity, there is no reason for Jasper and Zoe to disagree on how far she is above the floor (so z = z') or how far sideways she is from the aisle (so y = y'). Further, we've made the important assumption (for Galilean relativity) that their measurements of time are the same, so Zoe's time t' = t. So the transform equations for Galilean relativity (motion v in the x direction) are:
y = y', z = z', and t = t'.
a = a' For relativity, we need new transform equations because, as we have seen in Module 3, when v becomes comparable with the speed of light, Zoe and Jasper disagree on time and length.
Lorentz transform equationsSo, let's look for new transformation equations relating (x,y,z,t) and (x',y',z,t'). The motion is only in the x direction. They can again synchronise clocks: for convenience and symmetry, when they are side by side, they call that position zero and time zero. So x = 0 at t = 0 and x' = 0 at t' = 0. Further, at this moment, they can check that measurements in the y and z directions coincide, so two of the transformation equations are easy: y = y' and z = z'. Same as Galileo.However, we know that they disagree over time and length, so we need new transform equations for x and t. There is a good reason to try equations that are linear in x and t. First, we've seen that the time dilation and length contraction are linear in time and length. Second, if they are not linear, then we could end up have two solutions of x and t for a single event. This would be awkward for a frame that's travelling with constant velocity v! So let's write:
y' = y, z' = z, t' = Ct + Dx.
1 = γ2 - Dγv and so D = (γ2 - 1)/γv. 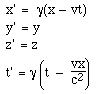 Addition of velocities in special relativityWhat about relative velocities? Now that we have the transformation equations, that is just a matter of taking derivatives. Let ux' be the x component of Zoe's velocity, measured in the train, and we have: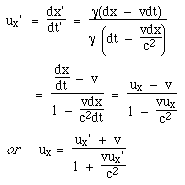 Imagine that a Vogon star ship travels towards Earth at v = c/2. The Vogon captain, with a poetic flourish, fires a sonnet (the name of a particularly dangerous Vogon armament) at Earth with speed of c/2, with respect to the star ship. With what relative speed does the sonnet travel towards Earth? Well this is just a case of substitution in the above equation, which yields: 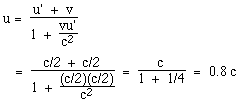 Okay, now cut to the chase. In one of the animations, Zoe (travelling at c/2) turns her headlights on, and both she and Jasper record their speed as c. Does that come out of these equations? 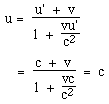 One further important observation. The equation for calculating relative velocities is non linear in ux', unless ux' is very much less than c. One important consequence of this is that, using the definition of momentum p = mu, we would find that momentum is not conserved. In relativity, we must use p = γmu so that p is conserved in the absence of external forces. An easy way to check this is to consider a symmetric inelastic collision in the two frames. We return to this in Energy in Newtonian mechanics and in relativity.
SpacetimeSo, under these transform equations, can our observers agree on anything? Well yes, there is one thing. Let's take an event (conventionally a spark, so it is well localised in time and space and radiates light in all directions) at (x,0,0,t) and another at (x1,0,0,t1). The quantity defined by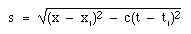 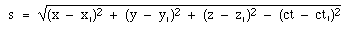 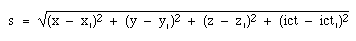 You will have noticed that time is different from the three spatial dimensions. To some extent, this 'specialness' of time appears in the fact that is an imaginary coordinate, and that it has the factor c in it. (Another way of saying the latter is that its natural units are inconveniently sized, or that human units of time and length, m/s, are suitable for speeds much slower than the natural speed in electromagnetism. i.e. a light second is much greater than a metre). But there is more. You can walk North or South with equal ease, and East and West. Travelling up and down are also possible. Time travel, on the other hand is easy in the forwards direction (we are all doing it) but not in the reverse. This takes us away from the physics that appears in this volume (electromagnetism, relativity, mechanics and quantum mechanics) and into thermal physics and the quantity entropy, whose symbol is S. S is related to heat and temperature, which in turn are related to energies distributed on the molecular scale. If you can arrange to do a thermal process in a way that is reversible, then the entropy of a system increases by ΔS where ΔS is the ratio ΔQ/T, i.e. the heat you add (ΔQ) divided by the temperature T at which you add it. The second law of thermodynamics can be stated in several ways. The way I like to state it is this 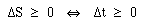
|
Home
| Summary
| Quiz
|
Credits
|
|