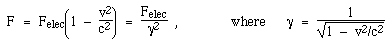The electric and magnetic forces between moving charges
|
Electricity and magnetism give insights into relativity, of course. Consider this example: I am running along the street at speed v. I am carrying a charge q in each hand. You are at rest in the street, and your natural reaction is to calculate the force between the two charges (which we shall do using classical electromagnetism).
Like gravity, the electric interaction is an inverse square law, and the force is proportional to the electric charge of each. The constant of proportionality depends on one's system of units. It is commonly written in one of two ways:
where kelec is the Coulomb constant for electricity, and where ε0 is the permittivity of free space. Although the second version of the constant is more common, we shall use both in parallel. This is partly for the benefit of those more familiar with one than the other, but also because the first version is helpful in an analogy we shall make. So, we write the expression for the electric repulsion as:
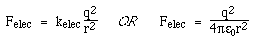 . .
|
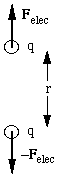
Electric force between two charges
|
Now consider the effect of the velocity v of the charges. Each moving charge is like a small element of electric current.
Like electricity*, the magnetic interaction is also an inverse square law, and the law of Biot-Savart gives the field B at distance r due to a small length dL carrying current I. For this geometry,
where kmag is Coulomb's constant for magnetism and μ0 is the permeability of space and where the direction is perpendicular to r and to v (out of the page, in this instance, for the field due to the upper charge at the position of the lower).
* Some people are surprised by this: expressions for electric field due to charges usually have the factor 1/r2 in them, whereas those for magnetic field due to a current usually have factor 1/r. The difference is due to the usual geometry: currents usually flow in long thin wires (approximately one dimensional things). Charges may be very small (approximately zero dimensional things). Calculating the field due to a one dimensional distribution involves an integration with respect to position along the wire, which usually removes a factor of r from the denominator. Note also that, in the Coulomb version for both forces, there is no 4π. Whether or not it appears depends on the definition of the constant. Aesthetically, it is appealing to have 4π precede r2: In this formulation, Gauss' law makes it clear that the inverse square law (in both cases) is a statement about the geometry of the universe, rather than some peculiar property of electromagnetism.
Now the term in parentheses is a pure number, so we can see that (kelec/kmag) or (1/μ0ε0) must have the units of speed squared. So let's write the preceding equation as:
 . .
This speed v0 is a critical value in this problem: if I could run at this speed, then the force you would calculate between the charges using this equation would be zero: the magnetic attraction would equal the electric repulsion.
So what is v0? If you have studied waves, the format of this expression may seem familiar. The speed of a wave is given by:
For example, the speed of a wave in a string and the speed of sound in a medium are respectively:
where F is the tension in the string, μ is its mass per unit length and where κ is the adiabatic bulk modulus of elasticity and ρ the density of the medium through which sound travels. κ is the ratio of the pressure difference applied to the fractional reduction in volume that it produces (and, in air, it is about 1.4 times the pressure of the air). Note that F and κ represent the property that returns a displacement of the string or the medium to equilibrium, and that the one and three dimensional densities μ and ρ represent the mass and thus the inertia, the capacity of the medium to overshoot the position of equilibrium. Both properties are required for an oscillation and for the transmission of a wave.
Now we are analysing an electromagnetic problem, so we might wonder whether v0 is the speed associated with the electromagnetic wave. Here, the medium for the wave is vacuum. In a sense, kelec represents its elastic or restoring property, because the electric field acts to move the charges so that it reduces the volume over which the field acts. In the same metaphorical way, kmag is analogous to inertia: Faraday's law tells us that a magnetic field, once established, can produce electrical effects that act to maintain the magnetic field.
Alternatively, we can go straight to Maxwell's equations, which tell us almost directly that the speed of light and other electromagnetic waves is:
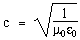 . .
So our equation for the total force between the two charges is:
In Special Relativity, the factor γ (or its reciprocal) appears regularly as the factor that relates physical measurements made in two inertial frames with relative speed v. In this case, the motion of the two charges reduces this force by a factor of γ2. So in this example, we could say that magnetism looks like the relativistic correction for electrostatics, when considering moving charges.
This naïve analysis does give some insight into the relation between electricity and magnetism, and more insight comes from the symmetry between electricity and magnetism in Maxwell's equations. In relativity, electromagnetic fields are often treated as vectors with six components, and that's what we should do here for a complete analys. But that is a whole new story.
How could a relativistic term produce such large forces?
My first reaction to the analysis above was surprise. We usually think of γ as a term that is very close to unity, except for velocities close to c. Yet currents with electron drift velocities very much smaller than c can produce large magnetic forces: for example, think of the electric motors that drive trains. How could a relativistic term produce such large forces?
Let me answer with an analogous question: how could gravity, which is such a puny force, govern the universe? The ratio of the electrical attraction between a proton and an electron to the gravitational attractions between them is 2 x 1039. Why isn't gravity negligible? The answer is, of course, that while there is no negative mass, there is negative charge. Consequently, on any large scale, electrical forces cancel out and gravity doesn't. If we removed the conduction electrons from two parallel wires (and somehow stopped the huge concentration of the remaining ions from exploding!), the electrostatic forces exerted between the ions in those two wires would be stupendous. However, they are neutralised by the presence of an equal negative charge carried by the electrons.
But not quite. At least, not if there are currents flowing. In this case, the repulsive forces between the moving electrons are reduced by a factor that is very, very slightly less than one: ie by (1/γ2). So, in the laboratory frame, we might say that the repulsive forces between the electrons in one wire and those in the other, plus that between the protons in the two wires, is very slightly less than the attractive force between the protons and the electrons. The calculated imbalance is then the magnetic force.
|
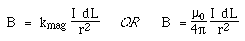
 .
.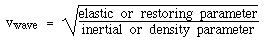
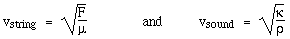
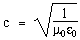 .
.